Transformers and Self-Attention

For the explanation of decoder-based architectures such as those used by GPT, please see the repo https://github.com/pantelis/femtotransformers and the embedded comments therein. A future version of this section will incorporate the commented source code from that repo as well as this popular repo that implements various other transformer architectures.

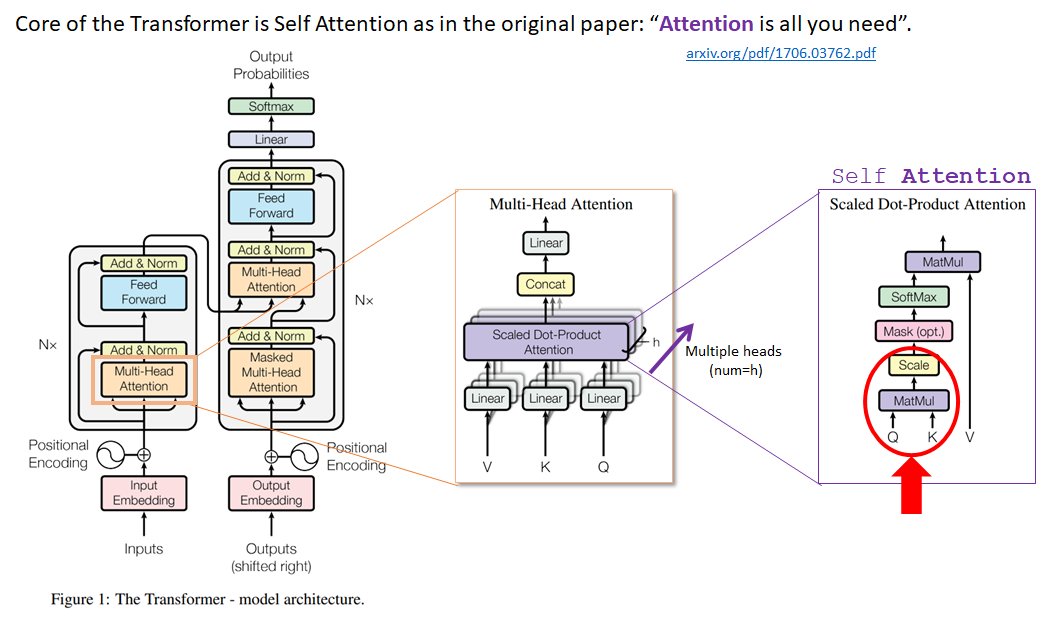
This is the original encoder-decoder architecture

As compared to the RNNs we have seen earlier, in the transformer architecture we:

1. Eliminate all recurrent connections present in earlier RNN architectures, therefore allowing the model to be trained as well as produce inference results much faster since we dont need to wait for the previous token to be processed. Because we broke the sequential nature of processing the input we need to encode explicitly the order that the token show up in the input context. This is done by adding positional encodings to the input embeddings.

2. Use attention mechanisms to allow the context-free embeddings, such as the word2vec embeddings, to be adjusted based on the context of the input sequence. These attention mechanisms will be present in the encoder or the decoder or in both encoder & decoder. We call this mechanism attention, since effectively each token attends to the other tokens of the input sequence that adjust mostly its embedding.

To understand the impact of self-attention, lets consider an example:

• I love bears
• She bears the pain
• Bears won the game

The self-attention mechanism, will change the vector that represents the token bears, from a point of the vector space that corresponds to a context-free representation, to another point that corresponds to a contextual representation i.e. includes the contributions of the other tokens. Obviously the token bears, has three different meanings in each of the above sentences: animal, tolerance and sports team. We should expect the vector mapping of the token to be different in each of the sentences to reflect that.

Simple self-attention mechanism

To achieve such mapping, we are enabling the other tokens to affect the initial coxtext-free representation via a simple dot-product mechanism that involves the input token \(x_i\) and all other tokens in the context. Such attention mechanism is called simple self-attention and the ‘self’ refers to the token’s dot product with itself and each and every other token of the input context.

This is shown in the next figure where we have formed the input context matrix \(X\) with dimensions [T, d] where \(T\) is the length of the input context and \(d\) is the embedding dimension. In this example a token is [dx1] vector with \(d=4\) and we have \(T=3\) tokens. Minimal realistic values for the size of such matrices are \(d=5120\) and \(T=4096\) (Llama-2), although higher values are typically used.

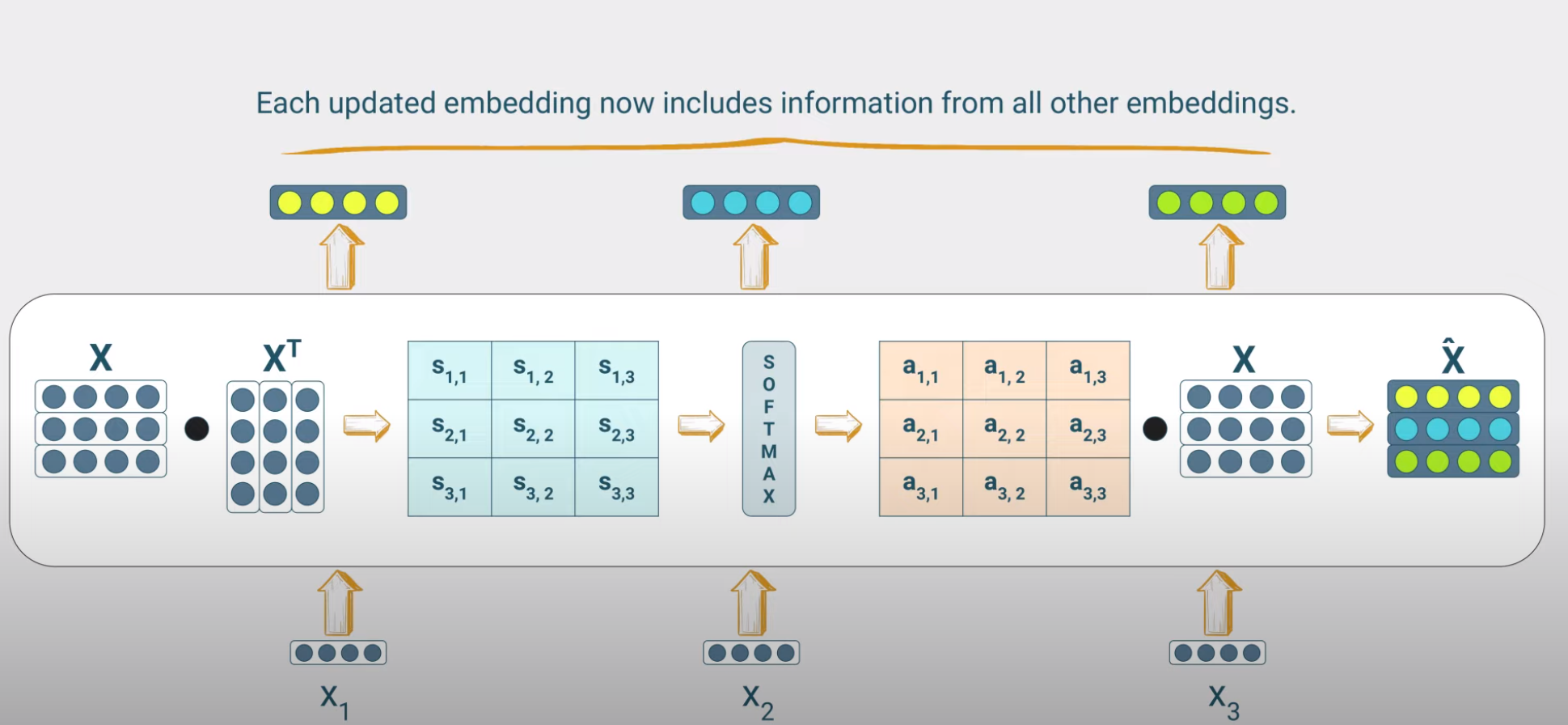
Typically the batch size \(B\) is also present, so we have \(X\) tensors with [B, T, d] dimensions but we will ignore batching in this initial treatment.

To implement the attention mechanism for example the \(i-th\) input token having embedding \(x_i\), we perform the following calculations:

Attention scores \(s_{ij}\) of the input token: These are computed as dot products of the embedding of the input token and each of the embeddings of the tokens of the input sentence (including the input token itself) indexed by \(j\). For example if the input sequence consists of 3 tokens, we will compute 3 attention scores for each token to finally obtain a 3x3 tensor.

Attention weights: The attention scores are then passed through a softmax function to obtain the corresponding attention weights. Recall that the softmax function is a vector input - vector output function that maps the input vector to a vector of values between 0 and 1, where the sum of all values is 1. So we apply the softmax across tokens of the context and expect to get 3 attention weights for each input token since T=3. Note that the softmax output has no probablilistic interpretation as it has in the context of classification tasks. Its an elegant way to make all attention weights positive and create a ‘competition’ amonst the tokens of the context.

\[a_{ij} \ge 0\] \[\sum_{j=1}^T a_{ij} = 1\]

A large attention score from one token, comes at the expense of the attention scores from the other tokens. In the limiting case, when the context is such that the \(i\) token attends 100% to itself, the input embedding vector remains unchanged since the attention weights of the other tokens towards this token are all zeros.

Output embedding : We then use the attention weights to create a weighted sum of the token embeddings of the input sequence to obtain the new input token embedding i.e. the embedding that now includes information from all other embeddings of the input sequence.

\[\hat x_i = \sum_{j=1}^T \alpha_{ij} x_j\]

where \(\alpha_{ij}\) is the attention weight of the \(j-th\) token of the input sequence for the \(i-th\) token of the input sequence of length T.

We can lump all the above steps into a single equation as shown below:

\[\hat X = \mathtt{softmax}(XX^T)X\]

At this point it may be beneficial to use an analogy to explain the self-attention mechanism.

Imagine you want to paint your room and you go to a retailer to buy the paint. At the store you consult a broshure and select the color of each room. Then you go to the kiosk ask (query) the attendant for this color. The attendant punches the code (key) written next to your desired color choice and the machine dispenses specific ammounts of black, red, green, blue, into a white can of paint that finally after spinning for few minutes, results into the color (value).

In this analogy the colors that fall into the white paint are the tokens that must be mixed while the ammounts correspond to the attention weights. We quoted some terms in bold that are the terms used in the more elaborate version of self-attention mechanism that we will address next.

Resources

1. An interesting video for the many attention mechanisms that are the roots of self-attention found in transformers.

2. Perhaps one of the best from scratch implementation of Transformers in Tensorflow.

```

```