Maximum Likelihood (ML) Estimation #

Most of the models in supervised machine learning are estimated using the ML principle. In this section we introduce the principle and outline the objective function of the ML estimator that has wide applicability in many learning tasks.

Learning marginal models - $p_{model}(\mathbf{x}; \mathbf w)$ #

Assume that we have $m$ examples drawn from a data generator that generates the vectors $\mathbf{x} \in \mathcal{X}$ independently and identically distributed (i.i.d.) according to some unknown (but fixed) probability distribution function $p_{data}(\mathbf{x})$.

$$\mathbb{X} = \{ \mathbf{x}_1, \dots, \mathbf{x}_m \}$$

Let $p_{model}(\mathbf x, \mathbf w)$ a parametric family of probability distributions (our hypothesis set) over the same space that attempts to approximate (model) $p_{data}(\mathbf{x})$ as closely as possible using a suitable estimate of the parameter vector $\mathbf w$. The ML estimator for $\mathbf w$ is defined as:

$$\bm w_{ML} = \argmax_{\mathbf w} p_{model}(\mathbb X; \mathbf w)$$ $$ = \argmax_{\mathbf w} \prod_{i=1}^m p_{model}(\mathbf x^{(i)}; \mathbf w)$$ $$ = \argmax_{\mathbf w} \sum_{i=1}^m \log p_{model}(\mathbf x^{(i)}; \mathbf w)$$ $$ = \argmax_{\mathbf w} \frac{1}{m} \sum_{i=1}^m \log p_{model}(\mathbf x^{(i)}; \mathbf w)$$ $$ = \argmax_{\mathbf w} \mathbb{E}_{\mathbf{x} \sim \hat p_{data}} \log p_{model}(\mathbf x; \mathbf w)$$

From the last expression it is evident that in ML estimation two distributions are involved: $\hat p_{data}$ and $p_{model}$. We can also make use of our intuition that a good estimator would minimize the distance between the two empirical distributions therefore the KL divergence:

$$KL( \hat p_{data} || p_{model} ) = \mathbb{E}_{\mathbf x \sim \hat p_{data}} [\log \hat p_{data}(\mathbf x) - \log p_{model}(\mathbf x, \mathbf w) ]$$

The 1st term is independent of the model and therefore we see that the KL and the ML estimator expressions are identical except from the sign. Therefore we conclude that minimizing KL divergence, maximizes the likelihood function. From information theory we know that the KL divergence and the cross entropy (CE) are related via the expression

$$CE = H(\hat p_{data}, p_{model}) = KL( \hat p_{data} || p_{model} ) + H(\hat p_{data})$$

Given that $\hat p_{data}$ is given in supervised learning, $H(\hat p_{data})$ is constant and therefore we can conclude that in this case, CE is equivalent to the KL i.e. **minimizing the KL divergence, is equivalent in minimizing cross-entropy (CE)**. Therefore the expression the only need to minimize which we will call the CE cost function (also known as log loss) is:

$$ L(\mathbf w) = CE = - \mathbb{E_{\mathbf x \sim \hat p_{data}}} \log p_{model}(\mathbf x, \mathbf w)$$

Cross entropy is a very generic objective (loss) function that is applicable to any supervised learning problem that uses maximum likelihood to estimate a model.

Learning conditional models - $\hat p_{model}(\mathbf y | \mathbf x; \mathbf w)$ #

The discussion in the marginal distribution is equivalently applicable to the conditional distribution $p_{model}(\mathbf y | \mathbf x, \mathbf w)$ which governs supervised learning, $y$ being the symbol of the label / target variable. Therefore all machine learning software frameworks offer excellent APIs on CE calculation.

$$ L(\mathbf w) = - \mathbb{E_{\mathbf x, \mathbf y \sim \hat p_{data}}} \log p_{model}(\mathbf y | \mathbf x; \mathbf w)$$

The attractiveness of the ML solution is that the CE (also known as log-loss) is general and we don’t need to re-design it when we change the model.

Example and implementation #

It is now instructive to go over an example to understand that even the plain-old mean squared error (MSE), the objective that is common in the regression setting, falls under the same umbrella - its the cross entropy between $\hat p_{data}$ and a Gaussian model.

Please follow the discussion associated with Section 5.5.1 of the Ian Goodfellow’s book or section 20.2.4 of Russell & Norvig’s book and these notes and consider the following figure for assistance to visualize the relationship of $p_{data}$ and $p_{model}$.

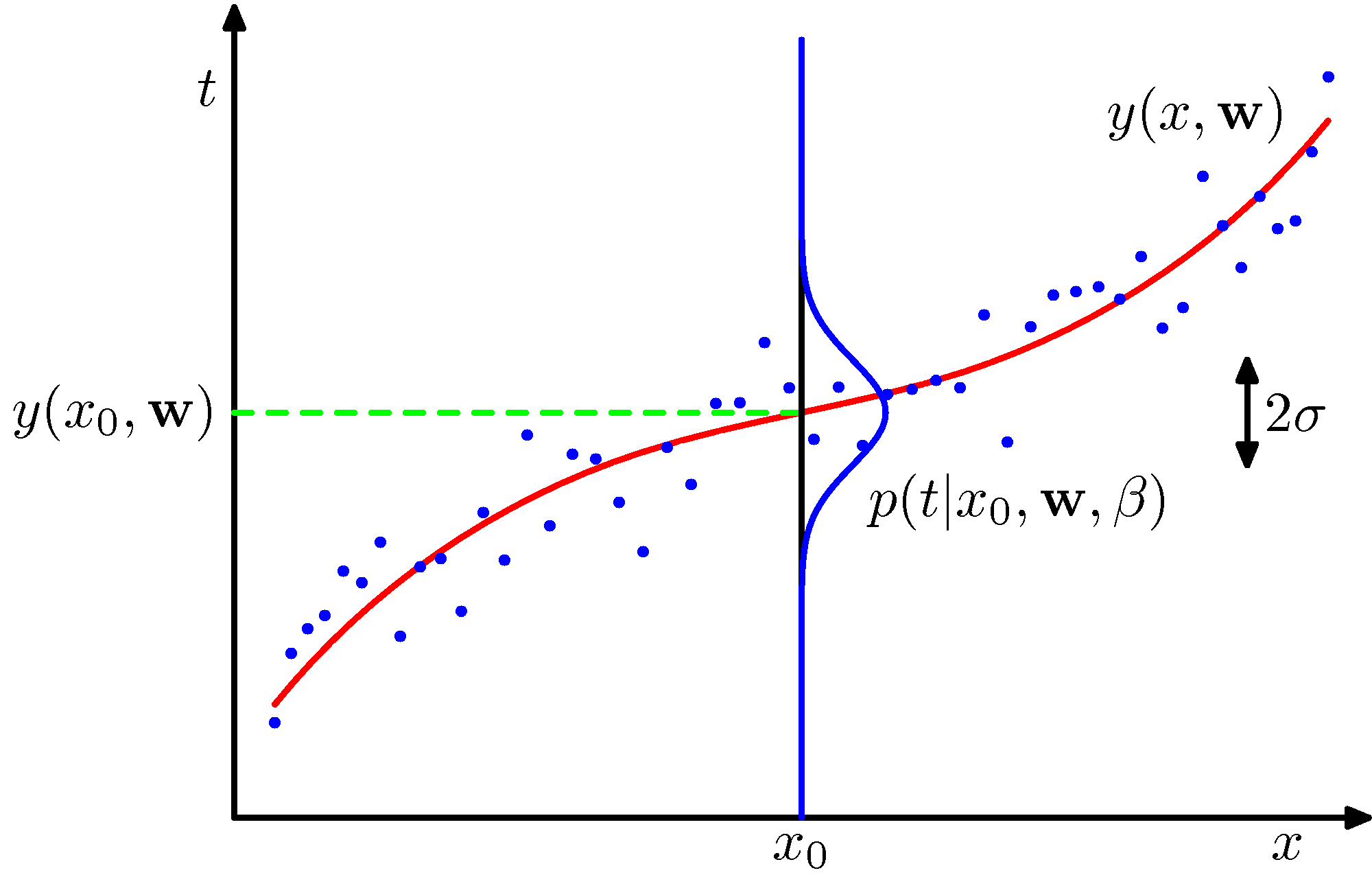Please replace the y-axis target variable $t$ with $y$. The green dashed line shows the mean of the $p{model}$ distribution._

The following notebook goes through the MLE calculation from scratch and shows the negative log-likelihood curves for a very simple MLE problem of fitting a Gaussian $p_{model}$ to an array produced by sampling an unknown underlying distribution $p_{data}$.

The following notebook is instructive of what MLE is calculating for the dataset we have seen before. Note that this notebook reveals also the large swings that the $\mathbf w$ takes to fit the model for larger capacities. Please vary $M$ in the code to observe the dynamic range of the weights of the model.

Optimal $\mathbf w$ for various model capacities