Vectors #

Most of the material in this section was borrowed from this excellent series of Essence of Linear Algebra youtube videos

The Physics, Computer Science and Math perspective on vectors #

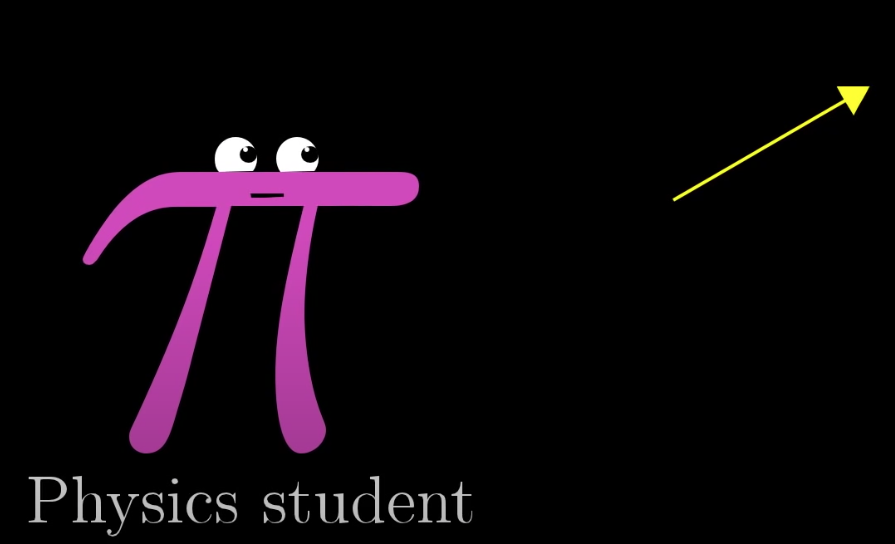
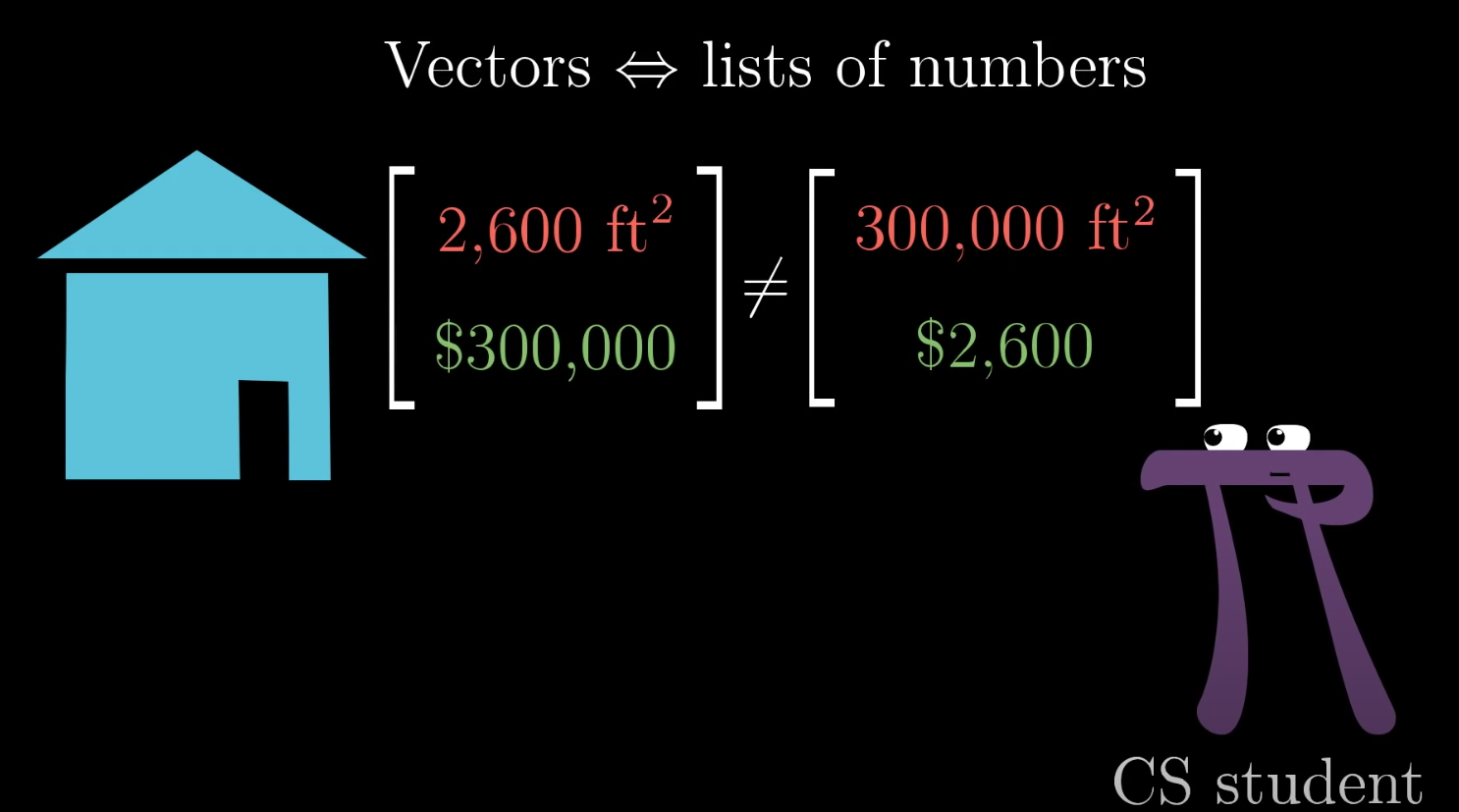
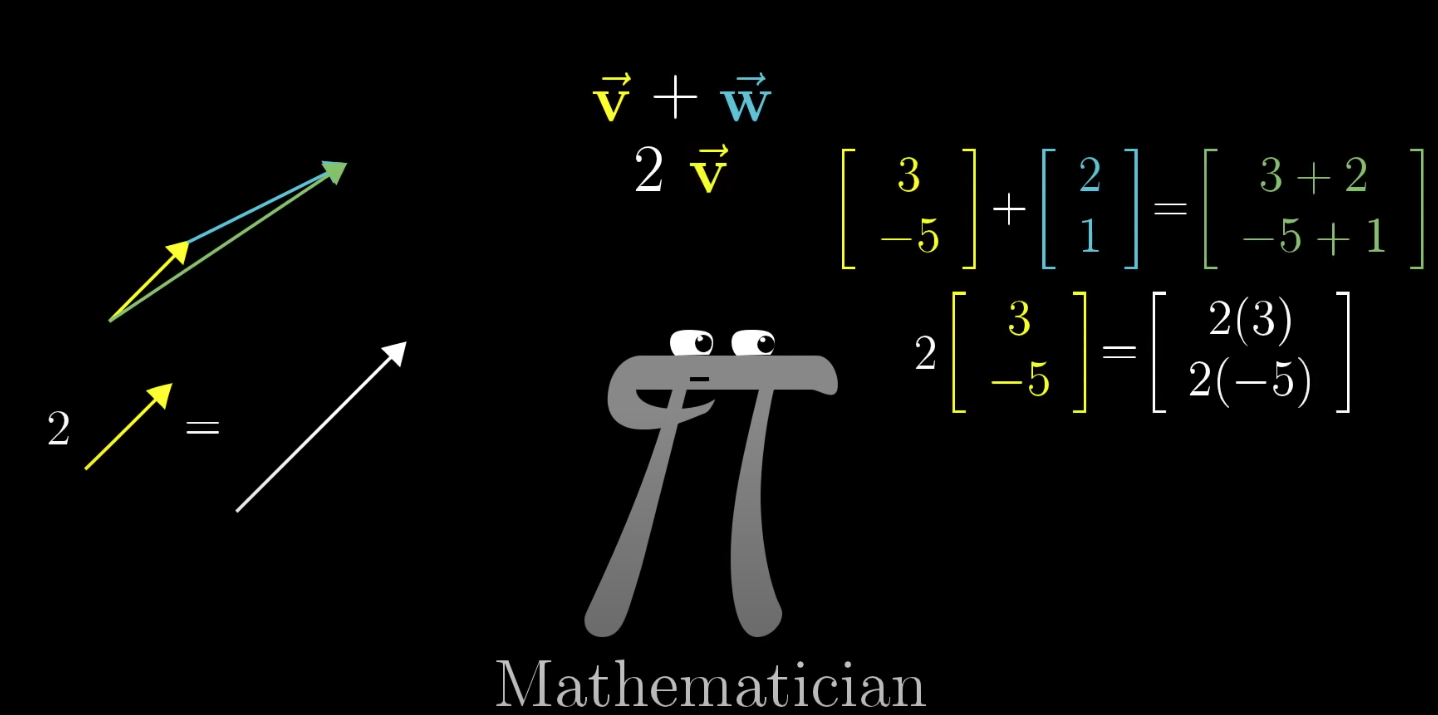
Coordinate systems and vector operations #

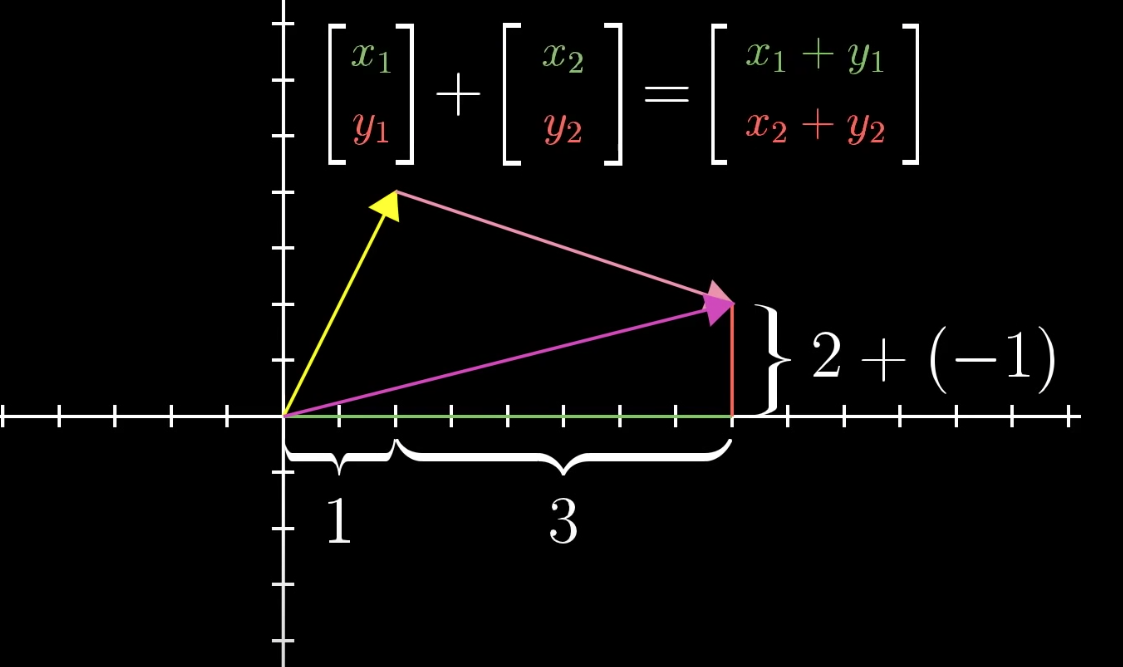Notice the typo - its $[x_1+x_2, y_1+y_2]$

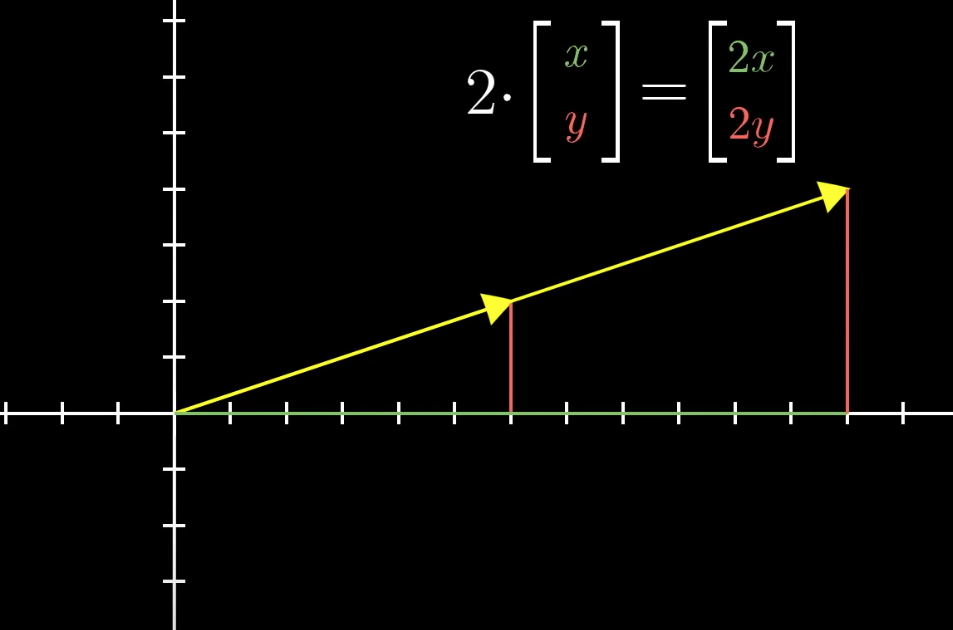
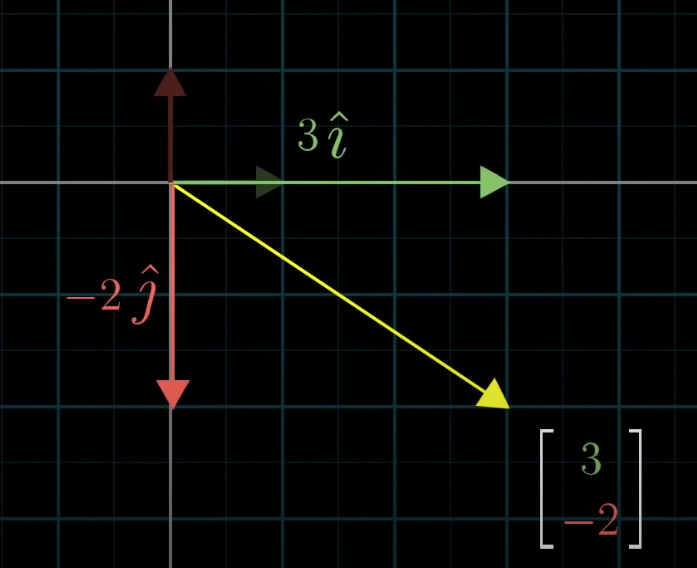$i$ and $j$ are the basis vectors of the xy coordinate system. But these are not the only basis vectors that we can have.

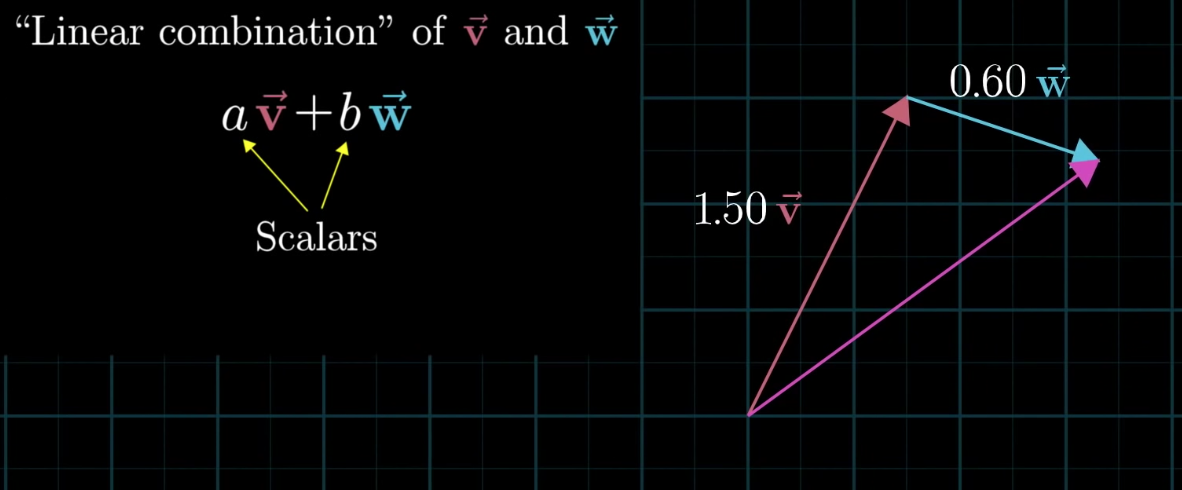Every 2D vector can be expressed as a linear combination of two vectors

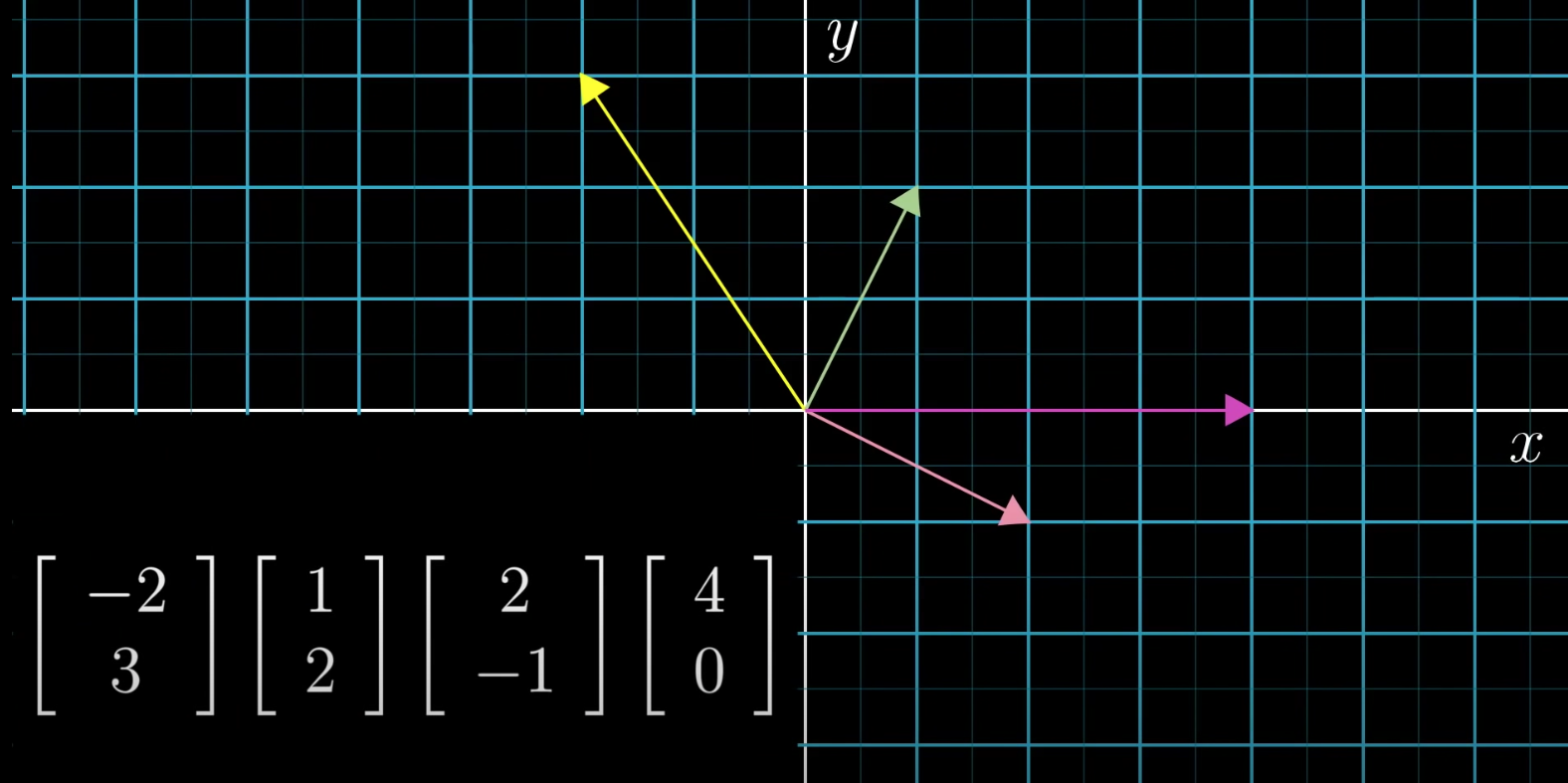
Not all vectors are good choices for creating a span. For example, these two vectors cant span the 2D space - they can only span a single line. $v$ and $w$ are then called linearly dependent.

These two vectors span the full 2D space - $v$ and $w$ are then called linearly independent.

Such set of vectors that are linearly independent and span the full space are called the basis vectors of a vector space