Probability Theory - Assignment A #

Exercise 1 (2 x 12.5 points) #

A data scientist develops a model of the mortality probability distribution function

$$p(t) = 3 \times 10^{-9} t^2(100-t)^2, 0 \le t \le 100 ~\text{years}$$

$p(t)$ is 0.0 outside the above range of $t$.

a. What is the probability that a person will die between 60 and 70.

b. What is the probability that a person will die between 60 and 70, given that was alive at 60.

Exercise 2 (2 x 12.5 points) #

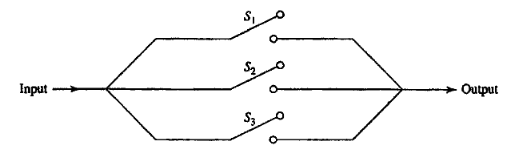
Three switches connected in parallel operate independently. Each switch remains closed with probability $p$.

a. Find the probability of receiving an input signal at the output.

b. Find the probability that switch $S_i$ is open given that an input signal is received at the output.

Exercise 3 (2 x 12.5 points) #

Make yourself familiar with the multinomial distribution

a. Each trial involves throwing a die with 10 faces/sides. All faces are equally probable aka the die is not biased. Calculate the probability of the counts of outcome “2” if we performed $n=1000$ trials.

b. Simulate n independent trials of the multinoulli (categorical distribution) compliant to the specification of (a). Plot the probability in (a) as a function of n independent trials (n=10-1000). Write your conclusions with respect to the behavior of the estimated probability as $n$ increases.

NOTE: Submit this exercise in a colab notebook with permissions set to the professor and grader to be able to view.

Exercise 4 (25 points) #

Replicate the Figure 1 plots of this writeup.

NOTE: Submit this exercise in a colab notebook with permissions set to the professor and grader to be able to view.