Matrices #
Most of the material in this section was borrowed from this excellent series of Essence of Linear Algebra youtube videos
Linear Transformation #
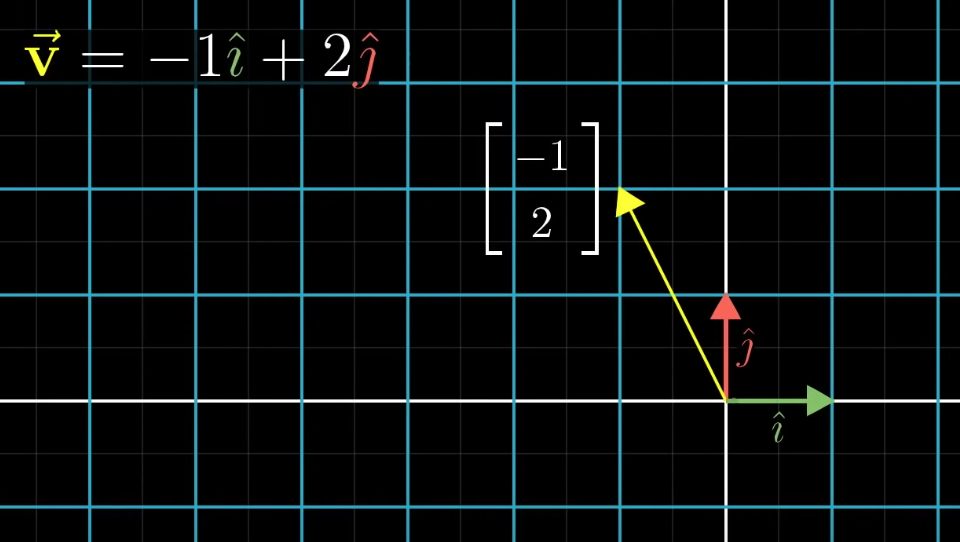
 The coordinates of the vector after a linear transformation are the same linear combination of the transformed basis vectors
The coordinates of the vector after a linear transformation are the same linear combination of the transformed basis vectors
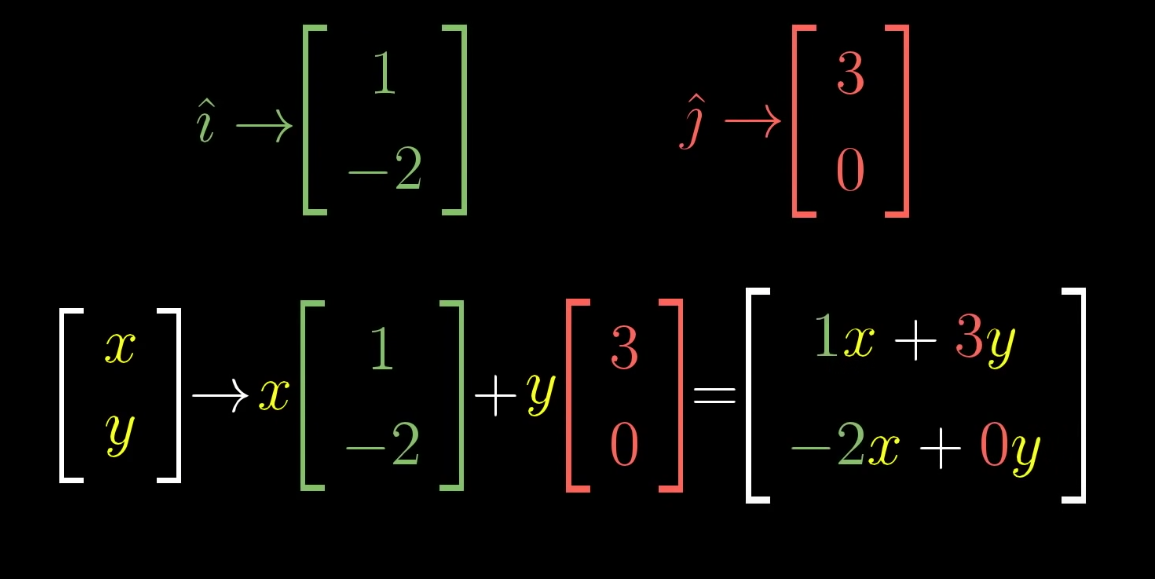
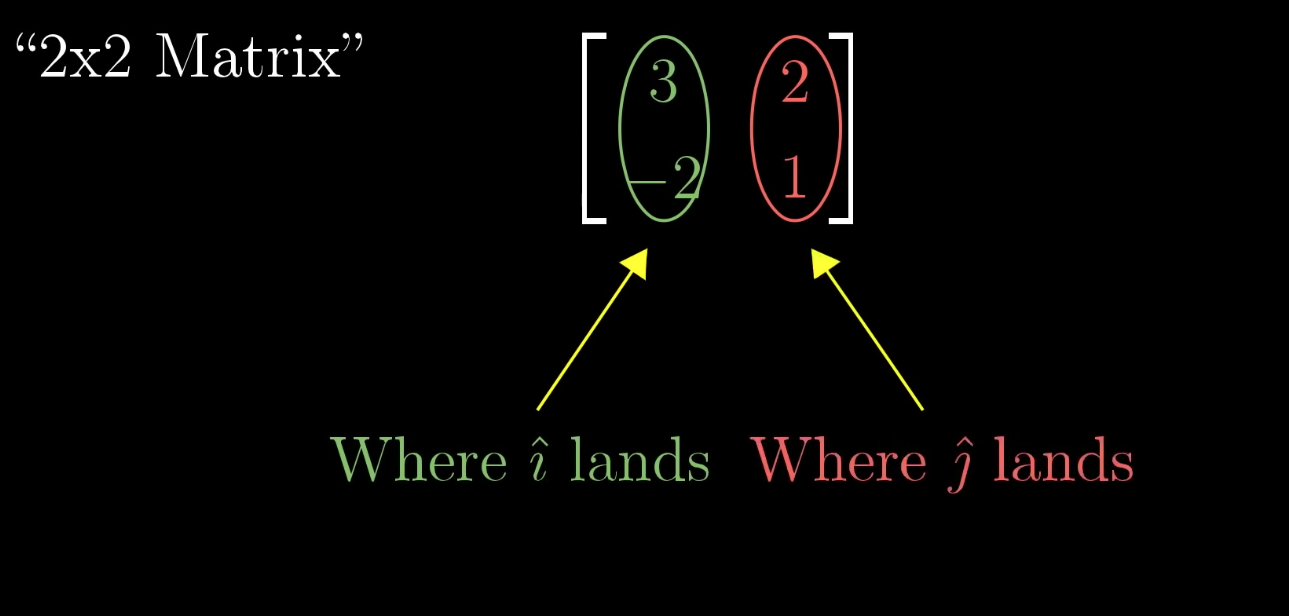 We can forma a matrix whose columns are the basis vectors
We can forma a matrix whose columns are the basis vectors
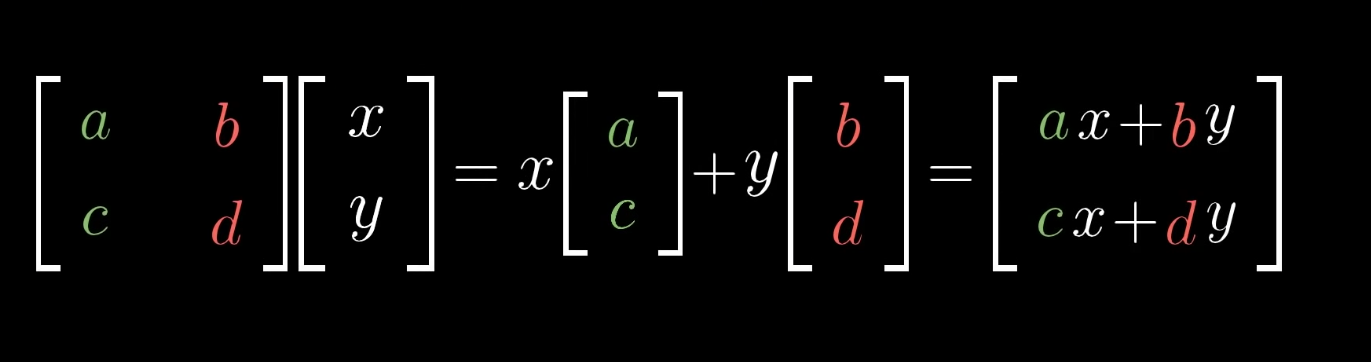 We can calculate the coordinates of the transformed vector via the basis matrix-vector multiplication
We can calculate the coordinates of the transformed vector via the basis matrix-vector multiplication
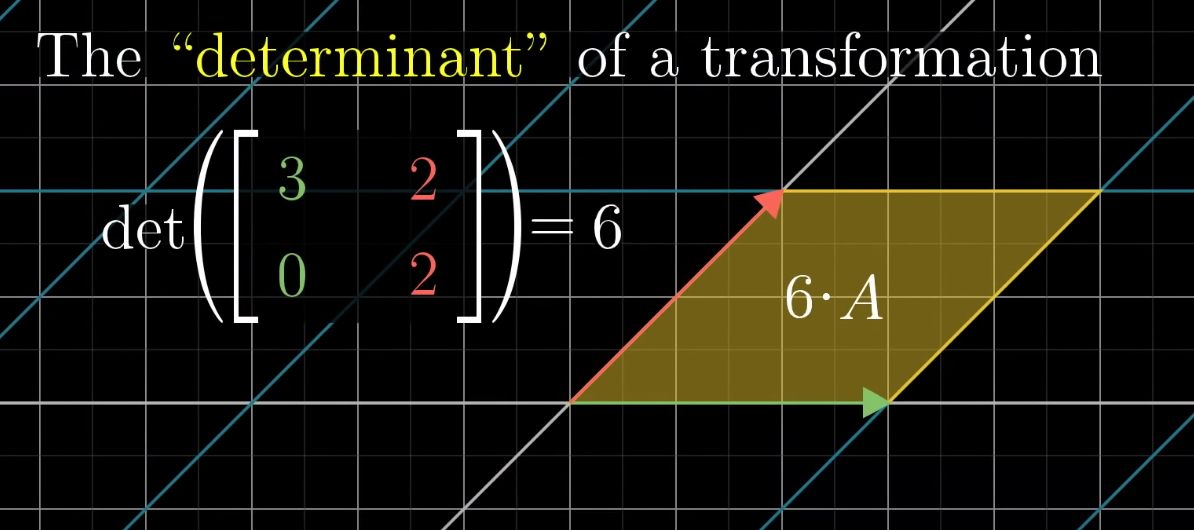 The factor by which the area after the transformation is increased.The sign of the dererminant indicates the “flipping” of the transformed space
The factor by which the area after the transformation is increased.The sign of the dererminant indicates the “flipping” of the transformed space
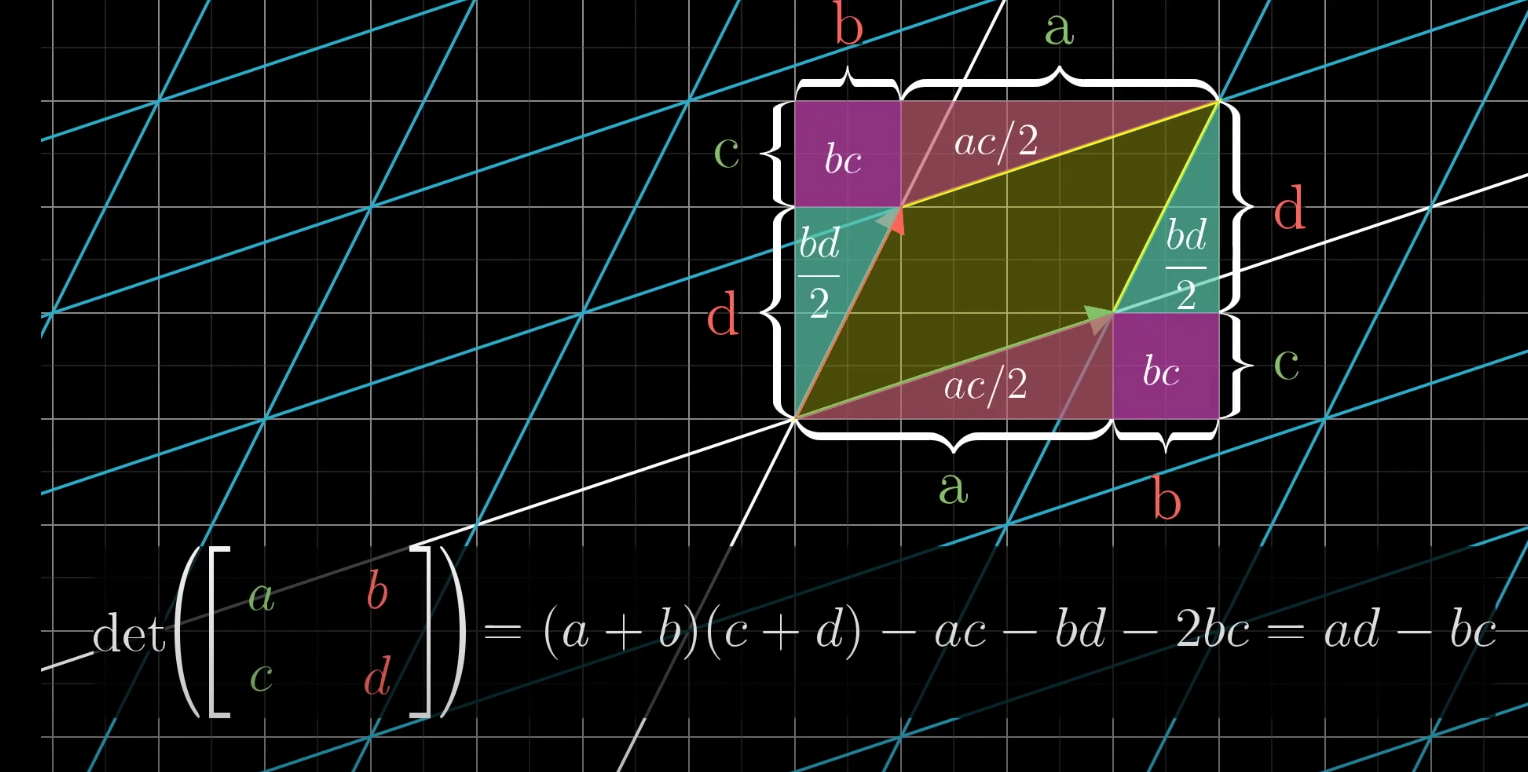 How to calculate the determinant.
How to calculate the determinant.
 The rank of the matrix is the positive integer that indicates the number of dimensions in the output of the transformation that involves this matrix.
The rank of the matrix is the positive integer that indicates the number of dimensions in the output of the transformation that involves this matrix.
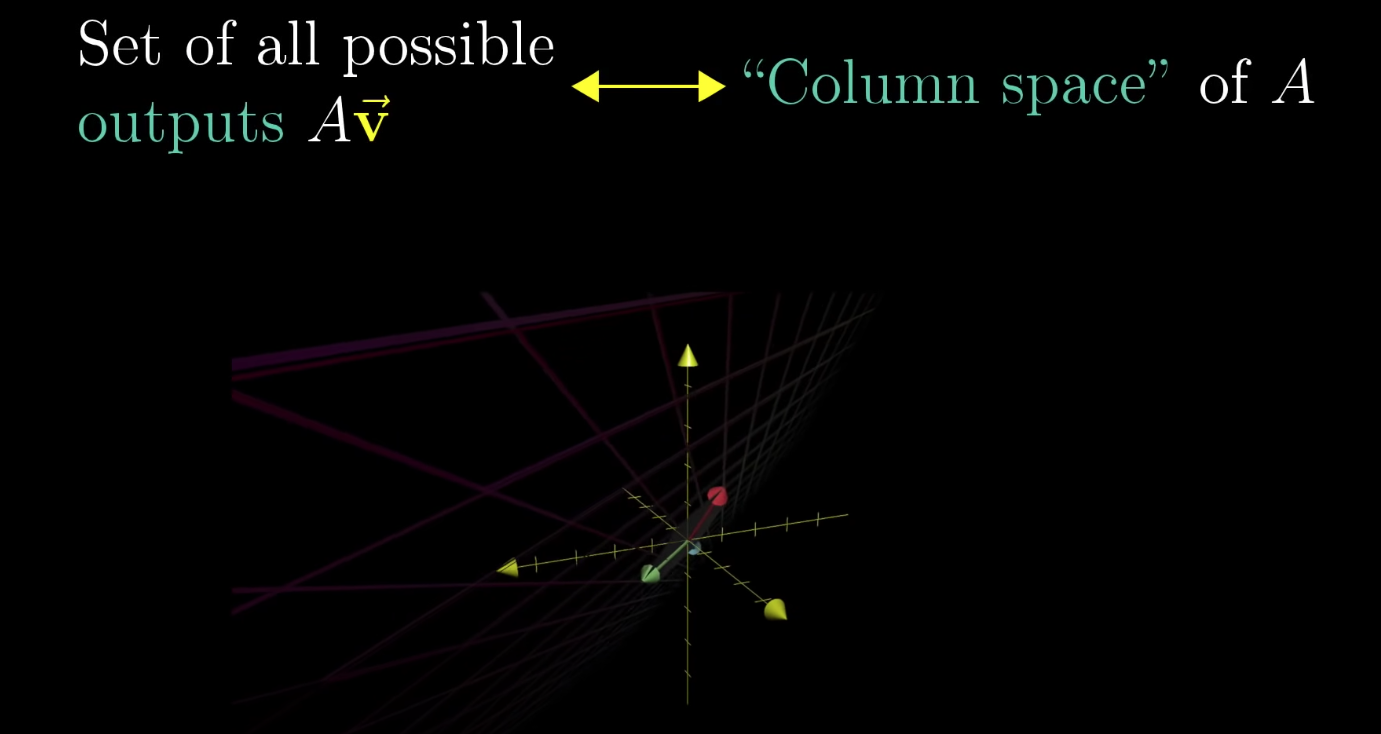 The column space is the span of its column vectors (input space)
The column space is the span of its column vectors (input space)
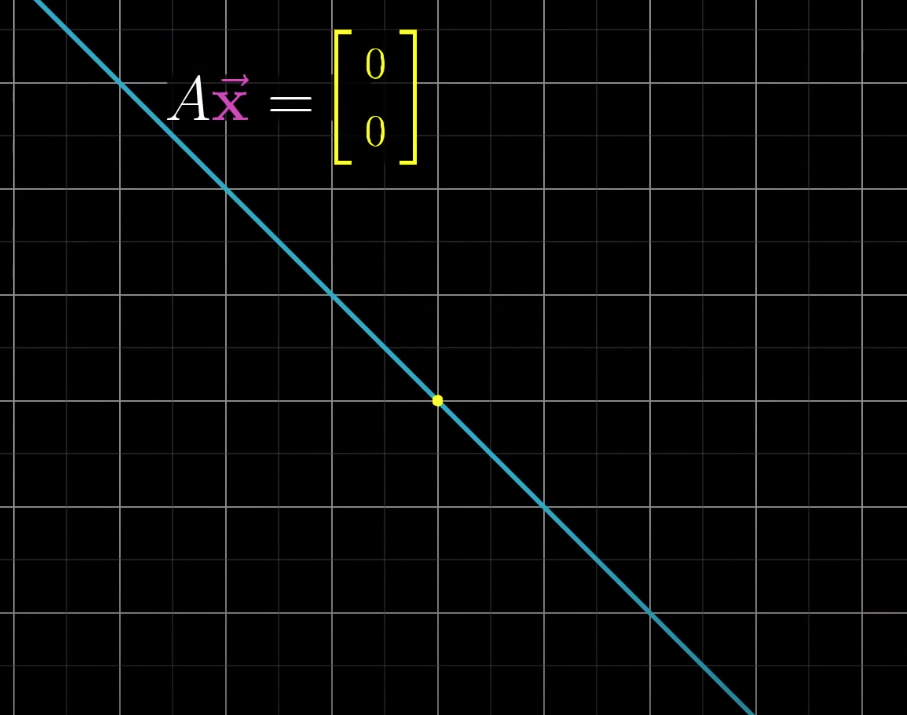 The null space is the space of all vectors that after the transformation land on the origin
The null space is the space of all vectors that after the transformation land on the origin
 2D to 3D transformation. The column space includes two basis vectors. Three rows indicate that the basis vectors live in 3D.
2D to 3D transformation. The column space includes two basis vectors. Three rows indicate that the basis vectors live in 3D.
Matrix Multiplication #
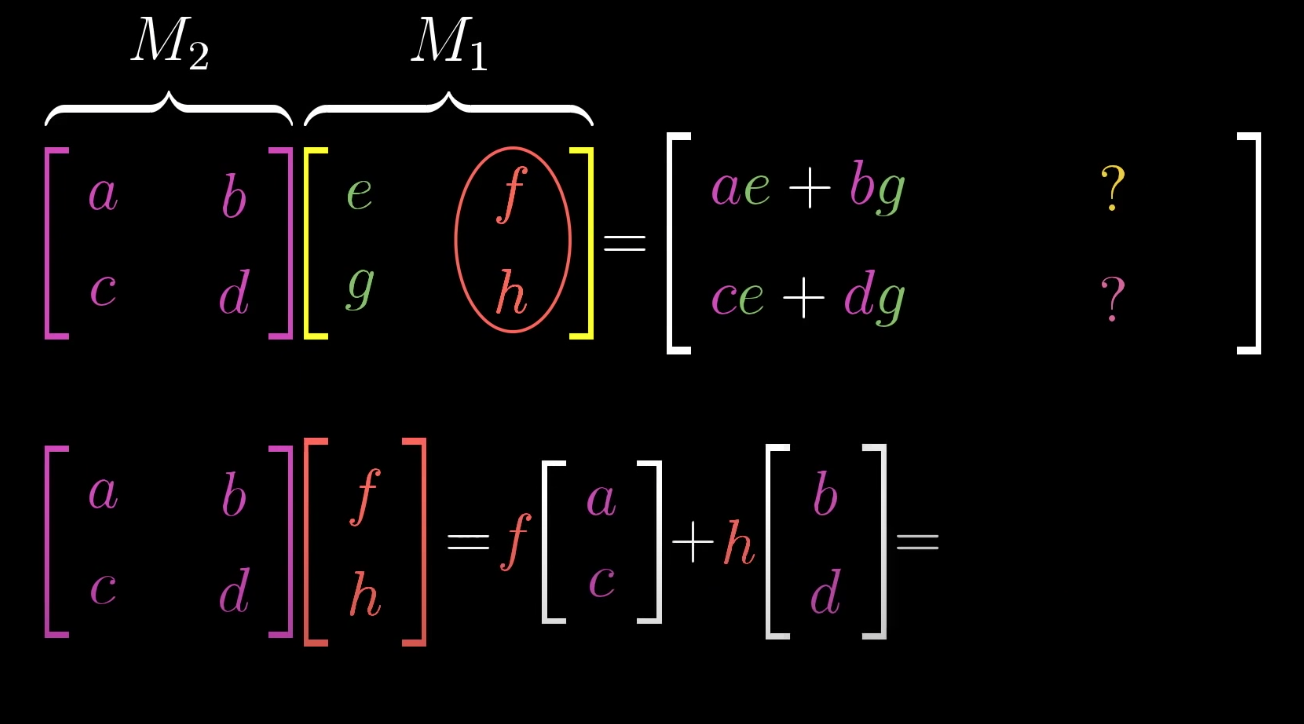 Matrix multiplication can be seen as two consecutive linear transformations
Matrix multiplication can be seen as two consecutive linear transformations
Inverse Matrices #
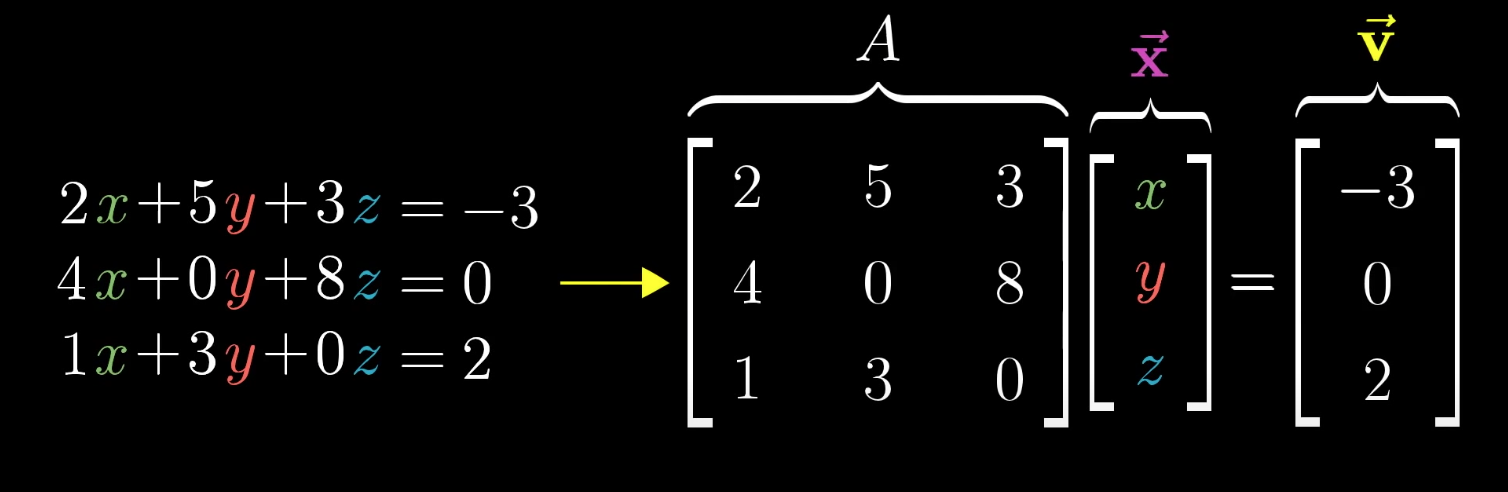
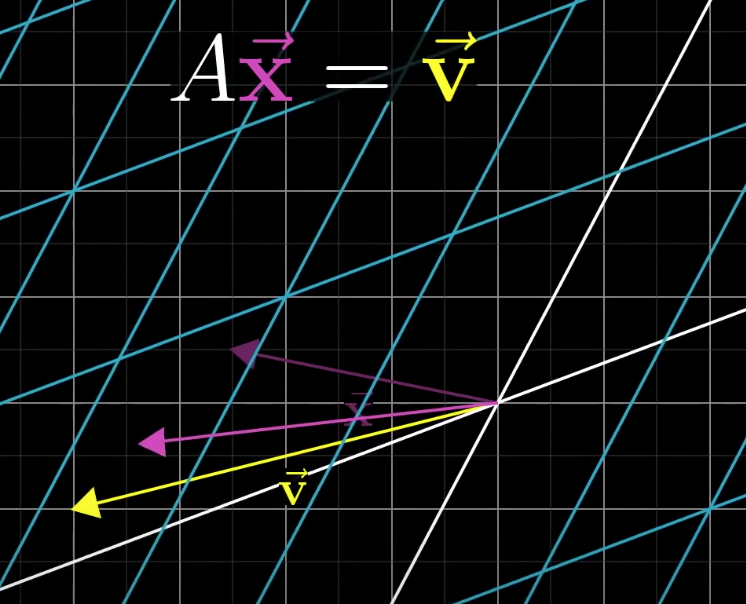 Looking for an $x$ that when it is transformed by $A$, it will land on $v$ - picture depicts multiple $x$’s not the solution that will be on top of $v$
Looking for an $x$ that when it is transformed by $A$, it will land on $v$ - picture depicts multiple $x$’s not the solution that will be on top of $v$
 Looking at the reverse problem, we can start with $v$ and find the transformation that gives us $x$.This transformation is called the inverse of $A$: $A^{-1}$
Looking at the reverse problem, we can start with $v$ and find the transformation that gives us $x$.This transformation is called the inverse of $A$: $A^{-1}$
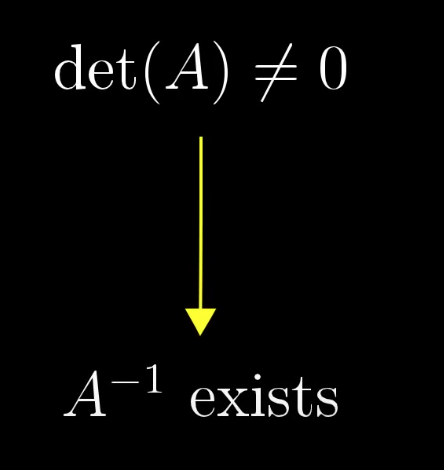 Existence of inverse transformation
Existence of inverse transformation
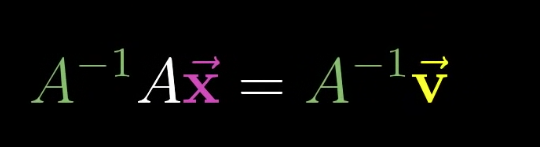 Solution to the linear system of equations
Solution to the linear system of equations