Policy Evaluation (Prediction)

The policy $π$ is evaluated when we have produced the state-value function $v_{π} (s)$ for all states. In other words when we know the expected discounted returns that each state can offer us.

Exact Solution (not recommended)

Suppose we have two states: $S = {s_{1}, s_{2}}$ , and a deterministic policy $π$ that always chooses action $a$ . The dynamics are:

From $s_{1}$ , action leads to $s_{2}$ with reward $2$
From $s_{2}$ , action leads to $s_{1}$ with reward $0$

Let $γ = 0.9$ and the state transition matrix under $π$ :

$P^{π} = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}]$

Reward vector:

$r^{π} = [\begin{matrix} 2 \\ 0 \end{matrix}]$

From the Bellman expectation equation:

$v^{π} = r^{π} + γ P^{π} v^{π}$

Rewriting:

$(I - γ P^{π}) v^{π} = r^{π}$

Compute:

$I - γ P^{π} = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] - 0.9 \cdot [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}] = [\begin{matrix} 1 & - 0.9 \\ - 0.9 & 1 \end{matrix}]$

Solve:

$[\begin{matrix} 1 & - 0.9 \\ - 0.9 & 1 \end{matrix}] [\begin{matrix} v_{1} \\ v_{2} \end{matrix}] = [\begin{matrix} 2 \\ 0 \end{matrix}]$

Solving gives:

$v_{1} = \frac{2 + 0.9 v_{2}}{1}, v_{2} = 0.9 v_{1} \Rightarrow v_{1} = 2 + 0.81 v_{1} \Rightarrow v_{1} (1 - 0.81) = 2 \Rightarrow v_{1} = \frac{2}{0.19} \approx 10.526, v_{2} \approx 9.474$

Iterative Policy Evaluation

This method is based on the recognition that the Bellman operator is contractive. We can apply the Bellman expectation backup equations repeatedly in an iterative fashion and converge to the state-value function of the policy.

We start at $k = 0$ by initializing all state-value function (a vector) to $v_{0} (s) = 0$ . In each iteration $k$ we start with the state value function of the previous iteration $v_{k} (s)$ and apply the Bellman expectation backup as prescribed by the one step lookahead tree below that is decorated relative to what we have seen in the Bellman expectation backup with the iteration information. This is called the synchronous backup formulation as we are updating all the elements of the value function vector at the same time.

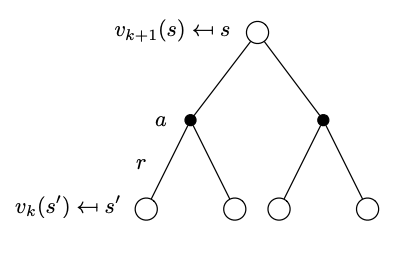policy-evaluation-tree Tree representation of the state-value function with one step look ahead across iterations.

The Bellman expectation backup is given by,

$v_{k + 1} (s) = \sum_{a \in A} π (a | s) (R_{s}^{a} + γ \sum_{s^{'} \in S} P_{s s^{'}}^{a} v_{k} (s^{'}))$

and in vector form,

$v^{k + 1} = R^{π} + γ P^{π} v^{k}$

Note

A simple scalar contraction that illustrates the idea behind iterative policy evaluation is:

$x_{k + 1} = c + γ x_{k}$

where: - $c$ is a constant (analogous to reward), - $γ \in [0, 1)$ is the contraction factor (analogous to the discount factor in MDPs).

This scalar recurrence mimics the vector version:

$v_{k + 1} = r^{π} + γ P^{π} v_{k}$

but in one dimension, where $P^{π}$ is just the scalar 1. Solving for the fixed point $x = c + γ x$ :

$x (1 - γ) = c \Rightarrow x = \frac{c}{1 - γ}$

Just like in policy evaluation, this converges because the operator $T (x) = c + γ x$ is a contraction mapping when $γ < 1$ .

# Scalar contraction example
c = 2
gamma = 0.9
x = 0

print("Scalar contraction iterations:\n")
for i in range(10):
    x = c + gamma * x
    print(f"Iteration {i+1}: x = {x}")

This will converge to $x = \frac{2}{1 - 0.9} = 20$ .

To implement the iterative approach to the MDP solution for the trivial two state problem, we start with initial guess:

$v_{0} = [\begin{matrix} 0 \\ 0 \end{matrix}]$

Update iteratively:

Iteration 1:

$v_{1} = r^{π} + γ P^{π} v_{0} = [\begin{matrix} 2 \\ 0 \end{matrix}] + 0.9 \cdot [\begin{matrix} 0 \\ 0 \end{matrix}] = [\begin{matrix} 2 \\ 0 \end{matrix}]$

Iteration 2:

$v_{2} = r^{π} + γ P^{π} v_{1} = [\begin{matrix} 2 \\ 0 \end{matrix}] + 0.9 \cdot [\begin{matrix} 0 \\ 2 \end{matrix}] = [\begin{matrix} 2 \\ 1.8 \end{matrix}]$

Iteration 3:

$P^{π} v_{2} = [\begin{matrix} 1.8 \\ 2 \end{matrix}] \Rightarrow v_{3} = [\begin{matrix} 2 \\ 0 \end{matrix}] + 0.9 \cdot [\begin{matrix} 1.8 \\ 2 \end{matrix}] = [\begin{matrix} 3.62 \\ 1.8 \end{matrix}]$

Iteration 4:

$P^{π} v_{3} = [\begin{matrix} 1.8 \\ 3.62 \end{matrix}] \Rightarrow v_{4} = [\begin{matrix} 2 \\ 0 \end{matrix}] + 0.9 \cdot [\begin{matrix} 1.8 \\ 3.62 \end{matrix}] = [\begin{matrix} 3.62 \\ 3.258 \end{matrix}]$

Continuing this will converge to:

$v^{π} \approx [\begin{matrix} 10.526 \\ 9.474 \end{matrix}]$

which matches the exact solution from the linear system.

Policy Evaluation - Minigrid Examples

The following examples are based on the minigrid - empty environment.

import numpy as np
import gymnasium as gym
from minigrid.wrappers import FullyObsWrapper
from copy import deepcopy
from collections import deque
import hashlib
import json


def build_minigrid_model(env):
    """
    Enumerate all reachable fully-observable states in MiniGrid,
    then build P[s,a,s'] and R[s,a]
    """
    # wrap to get full grid observation (no partial obs)
    env = FullyObsWrapper(env)
    # helper to hash an obs dictionary
    def obs_key(o):
        if isinstance(o, dict):
            # For dictionary observations, extract the 'image' part which is the grid
            if 'image' in o:
                return o['image'].tobytes()
            else:
                # If no 'image' key, convert dict to a stable string representation
                return hashlib.md5(json.dumps(str(o), sort_keys=True).encode()).hexdigest()
        else:
            # For array observations (older versions)
            return o.tobytes()

    # BFS over states
    state_dicts = []           # index -> env.__dict__ snapshot
    obs_to_idx = {}            # obs_key -> index
    transitions = {}           # (s,a) -> (s', r, done)

    # init
    obs, _ = env.reset(seed=0)
    idx0 = 0
    obs_to_idx[obs_key(obs)] = idx0
    state_dicts.append(deepcopy(env.unwrapped.__dict__))
    queue = deque([obs])

    while queue:
        obs = queue.popleft()
        s = obs_to_idx[obs_key(obs)]
        # restore that state
        env.unwrapped.__dict__.update(deepcopy(state_dicts[s]))

        for a in range(env.action_space.n):
            obs2, r, terminated, truncated, _ = env.step(a)
            done = terminated or truncated

            key2 = obs_key(obs2)
            if key2 not in obs_to_idx:
                obs_to_idx[key2] = len(state_dicts)
                state_dicts.append(deepcopy(env.unwrapped.__dict__))
                queue.append(obs2)

            s2 = obs_to_idx[key2]
            transitions[(s,a)] = (s2, r, done)

            # restore before next action
            env.unwrapped.__dict__.update(deepcopy(state_dicts[s]))

    nS = len(state_dicts)
    nA = env.action_space.n

    # build P and R arrays
    P = np.zeros((nS, nA, nS), dtype=np.float32)
    R = np.zeros((nS, nA), dtype=np.float32)
    for (s,a), (s2, r, done) in transitions.items():
        if done:
            # absorbing: stay in s
            P[s,a,s] = 1.0
        else:
            P[s,a,s2] = 1.0
        R[s,a] = r

    return P, R, state_dicts

Exact Solution (not recommended)

def solve_policy_linear_minigrid(env, gamma=0.9):
    """
    Under uniform random policy, solve (I - γ P^π) v = R^π exactly.
    """
    P, R, state_dicts = build_minigrid_model(env)
    nS, nA = R.shape

    # uniform random policy
    pi = np.ones((nS, nA)) / nA

    # build P^π and R^π
    P_pi = np.einsum('sa,sab->sb', pi, P)  # shape (nS,nS) - fixed indices to avoid repeated output subscript
    R_pi = (pi * R).sum(axis=1)            # shape (nS,)

    # solve linear system
    A = np.eye(nS) - gamma * P_pi
    v = np.linalg.solve(A, R_pi)
    return v, state_dicts

if __name__ == "__main__":
    # 1. create the Minigrid env
    env = gym.make("MiniGrid-Empty-5x5-v0")

    # 2. solve for v under random policy
    v, states = solve_policy_linear_minigrid(env, gamma=0.99)  # Changed from 1.0 to 0.99

    # 3. print out values by (pos,dir)
    print("State-value function for each (x,y,dir):\n")
    for idx, sdict in enumerate(states):
        pos = sdict['agent_pos']
        d   = sdict['agent_dir']
        print(f"  s={idx:2d}, pos={pos}, dir={d}:  V = {v[idx]:6.3f}")

Iterative Method

import numpy as np
import gymnasium as gym
from minigrid.wrappers import FullyObsWrapper

def policy_eval_iterative(env, policy, discount_factor=0.99, epsilon=0.00001):
    """
    Evaluate a policy given an environment using iterative policy evaluation.
    
    Args:
        policy: [S, A] shaped matrix representing the policy.
        env: MiniGrid environment
        discount_factor: Gamma discount factor.
        epsilon: Threshold for convergence.
    
    Returns:
        Vector representing the value function.
    """
    # Build model to get state space size and transition probabilities
    P, R, state_dicts = build_minigrid_model(env)
    nS, nA = R.shape
    
    # Start with zeros for the value function
    V = np.zeros(nS)
    
    while True:
        delta = 0
        # For each state, perform a "full backup"
        for s in range(nS):
            v = 0
            # Look at the possible next actions
            for a, action_prob in enumerate(policy[s]):
                # For each action, look at the possible next states
                for s_next in range(nS):
                    # If transition is possible
                    if P[s, a, s_next] > 0:
                        # Calculate the expected value
                        v += action_prob * P[s, a, s_next] * (R[s, a] + discount_factor * V[s_next])
            # How much did the value change?
            delta = max(delta, np.abs(v - V[s]))
            V[s] = v
        # Stop evaluating once our value function change is below threshold
        if delta < epsilon:
            break
            
    return V

# Create the MiniGrid environment
env = gym.make("MiniGrid-Empty-5x5-v0")
env = FullyObsWrapper(env)

# Get model dimensions
P, R, state_dicts = build_minigrid_model(env)
nS, nA = R.shape

# Create a uniform random policy
random_policy = np.ones([nS, nA]) / nA

# Evaluate the policy
v = policy_eval_iterative(env, random_policy, discount_factor=0.99)

# Print results
print("State-value function using iterative policy evaluation:\n")
for idx, sdict in enumerate(state_dicts):
    pos = sdict['agent_pos']
    d   = sdict['agent_dir']
    print(f"  s={idx:2d}, pos={pos}, dir={d}:  V = {v[idx]:6.3f}")

State-value function using iterative policy evaluation:

  s= 0, pos=(1, 1), dir=0:  V =  0.923
  s= 1, pos=(1, 1), dir=3:  V =  0.862
  s= 2, pos=(1, 1), dir=1:  V =  0.923
  s= 3, pos=(2, 1), dir=0:  V =  1.050
  s= 4, pos=(1, 1), dir=2:  V =  0.862
  s= 5, pos=(1, 2), dir=1:  V =  1.048
  s= 6, pos=(2, 1), dir=3:  V =  0.961
  s= 7, pos=(2, 1), dir=1:  V =  1.060
  s= 8, pos=(3, 1), dir=0:  V =  1.204
  s= 9, pos=(1, 2), dir=0:  V =  1.060
  s=10, pos=(1, 2), dir=2:  V =  0.959
  s=11, pos=(1, 3), dir=1:  V =  1.199
  s=12, pos=(2, 1), dir=2:  V =  0.939
  s=13, pos=(2, 2), dir=1:  V =  1.267
  s=14, pos=(3, 1), dir=3:  V =  1.121
  s=15, pos=(3, 1), dir=1:  V =  1.372
  s=16, pos=(1, 2), dir=3:  V =  0.938
  s=17, pos=(2, 2), dir=0:  V =  1.269
  s=18, pos=(1, 3), dir=0:  V =  1.366
  s=19, pos=(1, 3), dir=2:  V =  1.117
  s=20, pos=(2, 2), dir=2:  V =  1.076
  s=21, pos=(2, 3), dir=1:  V =  1.547
  s=22, pos=(3, 1), dir=2:  V =  1.118
  s=23, pos=(3, 2), dir=1:  V =  1.892
  s=24, pos=(2, 2), dir=3:  V =  1.076
  s=25, pos=(3, 2), dir=0:  V =  1.554
  s=26, pos=(1, 3), dir=3:  V =  1.114
  s=27, pos=(2, 3), dir=0:  V =  1.881
  s=28, pos=(2, 3), dir=2:  V =  1.321
  s=29, pos=(3, 2), dir=2:  V =  1.398
  s=30, pos=(3, 3), dir=1:  V =  1.087
  s=31, pos=(3, 2), dir=3:  V =  1.327
  s=32, pos=(2, 3), dir=3:  V =  1.393
  s=33, pos=(3, 3), dir=0:  V =  1.088
  s=34, pos=(3, 3), dir=2:  V =  1.164
  s=35, pos=(3, 3), dir=3:  V =  1.165

Policy Evaluation using Ray

The problem here is trivial and in practice Ray is often used to parallelize computations. For more information see the Ray documentation and Ray RLlib

import torch
import ray
import numpy as np
import gymnasium as gym
from minigrid.wrappers import FullyObsWrapper

ray.init()  # start Ray (will auto-detect cores)

@ray.remote
def eval_state(s, V_old, policy_s, P, R, gamma, epsilon):
    """
    Compute the new V[s] for a single state s under `policy_s`
    V_old: torch tensor (nS,)
    policy_s: torch tensor (nA,)
    P: Transition probability array of shape (nS, nA, nS)
    R: Reward array of shape (nS, nA)
    """
    v = 0.0
    for a, π in enumerate(policy_s):
        for s_next in range(len(V_old)):
            # If transition is possible
            if P[s, a, s_next] > 0:
                # Calculate expected value
                v += π * P[s, a, s_next] * (R[s, a] + gamma * V_old[s_next])
    return float(v)

def policy_eval_ray_minigrid(env, policy, gamma=0.99, epsilon=1e-5):
    """
    Policy evaluation using Ray for parallel computation in MiniGrid
    """
    # Build model to get transitions and rewards
    P, R, state_dicts = build_minigrid_model(env)
    nS, nA = R.shape
    
    # torch tensors for GPU/CPU flexibility
    V_old = torch.zeros(nS, dtype=torch.float32)
    policy_t = torch.tensor(policy, dtype=torch.float32)

    while True:
        # launch one task per state
        futures = [
            eval_state.remote(
                s,
                V_old,
                policy_t[s],
                P,
                R,
                gamma,
                epsilon
            )
            for s in range(nS)
        ]
        # gather all new V's
        V_new_list = ray.get(futures)
        V_new = torch.tensor(V_new_list)

        # check convergence
        if torch.max(torch.abs(V_new - V_old)) < epsilon:
            break
        V_old = V_new

    return V_new

if __name__ == "__main__":
    # Create the MiniGrid environment
    env = gym.make("MiniGrid-Empty-5x5-v0")
    env = FullyObsWrapper(env)

    # Get model dimensions
    P, R, state_dicts = build_minigrid_model(env)
    nS, nA = R.shape
    
    # uniform random policy
    random_policy = np.ones((nS, nA)) / nA
    
    # evaluate policy using Ray parallel computation
    v = policy_eval_ray_minigrid(env, random_policy, gamma=0.99)
    
    # Print results in the same format as cell 1
    print("State-value function using Ray parallel evaluation:\n")
    for idx, sdict in enumerate(state_dicts):
        pos = sdict['agent_pos']
        d   = sdict['agent_dir']
        print(f"  s={idx:2d}, pos={pos}, dir={d}:  V = {v[idx]:6.3f}")

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
Cell In[2], line 7
      4 import gymnasium as gym
      5 from minigrid.wrappers import FullyObsWrapper
----> 7 ray.init()  # start Ray (will auto-detect cores)
      9 @ray.remote
     10 def eval_state(s, V_old, policy_s, P, R, gamma, epsilon):
     11     """
     12     Compute the new V[s] for a single state s under `policy_s`
     13     V_old: torch tensor (nS,)
   (...)     16     R: Reward array of shape (nS, nA)
     17     """

File /workspaces/engineering-ai-agents/.venv/lib/python3.11/site-packages/ray/_private/client_mode_hook.py:103, in client_mode_hook.<locals>.wrapper(*args, **kwargs)
    101     if func.__name__ != "init" or is_client_mode_enabled_by_default:
    102         return getattr(ray, func.__name__)(*args, **kwargs)
--> 103 return func(*args, **kwargs)

File /workspaces/engineering-ai-agents/.venv/lib/python3.11/site-packages/ray/_private/worker.py:1676, in init(address, num_cpus, num_gpus, resources, labels, object_store_memory, local_mode, ignore_reinit_error, include_dashboard, dashboard_host, dashboard_port, job_config, configure_logging, logging_level, logging_format, logging_config, log_to_driver, namespace, runtime_env, storage, **kwargs)
   1674         return RayContext(dict(_global_node.address_info, node_id=node_id.hex()))
   1675     else:
-> 1676         raise RuntimeError(
   1677             "Maybe you called ray.init twice by accident? "
   1678             "This error can be suppressed by passing in "
   1679             "'ignore_reinit_error=True' or by calling "
   1680             "'ray.shutdown()' prior to 'ray.init()'."
   1681         )
   1683 _system_config = _system_config or {}
   1684 if not isinstance(_system_config, dict):

RuntimeError: Maybe you called ray.init twice by accident? This error can be suppressed by passing in 'ignore_reinit_error=True' or by calling 'ray.shutdown()' prior to 'ray.init()'.