Finding optimal policies in Gridworld

Non-deterministic outcomes

  • The environment is stochastic yet fully observable.
  • Due to uncertainty, an action causes transition from state to another state with some probability. There is no dependence on previous states.
  • We now have a sequential decision problem for a fully observable, stochastic environment with Markovian transition model and additive rewards consisting of:
    • a set of states \(S\). State at time \(t\) is \(s_t\)
    • actions \(A\). Action at time \(t\) is \(a_t\).
    • transition model describing outcome of each action in each state \(P( s_{t+1} | s_t,a_t)\)
    • reward function \(r_t=R(s_t)\)

MDP Transition Model

Agent-Environment Interaction with Rewards

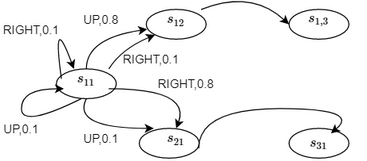
Partial Transition Graph (A) 4x3 Maze

  • Transition Model Graph:
    • Each node is a state.
    • Each edge is the probability of transition

Utility for MDP

Robot in \((3,3)\) of Maze
  • Since we have stochastic environment, we need to take into account the transition probability matrix
  • Utility of a state is the immediate reward of the state plus the expected discounted utility of the next state due to the action taken
  • Bellman’s Equations: if we choose an action \(a\) then

\(U(s) = R(s) + \gamma \sum_{s^{'}} P(s^{'}| s,a)U(s^{'})\)

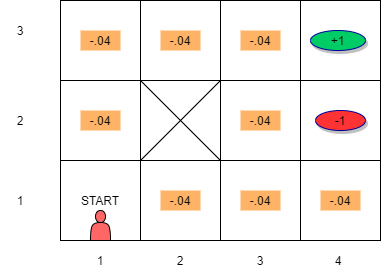
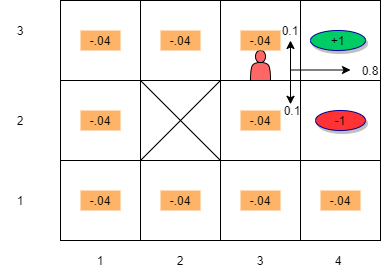
Robot in (3,3) of Maze

  • Suppose robot is in state \(s_{33}\) and the action taken is “RIGHT”. Also assume \(\gamma = 1\)
  • We want to compute the utility of this state: \[ U(s_{33}) = R(s_{33}) + \gamma (P(s_{43} | s_{33}, \rightarrow) U(s_{43}) + P(s_{33} | s_{33}, \rightarrow) U(s_{33}) + P(s_{32} | s_{33}, \rightarrow) U(s_{32}))\]
  • Substituting we get:

\[U(s_{33}) = R(s_{33}) + \gamma ( (0.8 \times U(s_{43})) + (0.1 \times U(s_{33})) + (0.1 \times U(s_{23})))\]

Policy for MDP

  • If we choose action \(a\) that maximizes future rewards, \(U(s)\) is the maximum we can get over all possible choices of actions and is represented as \(U^{*}(s)\).

  • We can write this as \[U^*(s) = R(s) + \gamma \underset{a}{ \max} (\sum_{s^{'}} P(s^{'}| s,a)U(s'))\]

  • The optimal policy (which recommends \(a\) that maximizes U) is given by:

\[\pi^{*}(s) = \underset{a}{\arg \max}(\sum_{s^{'}} P(s^{'}| s,a)U^{*}(s^{'}))\]

  • Can the above \(2\) be solved directly?

    • The set of \(|S|\) equations for \(U^*(s)\) cannot be solved directly because they are non-linear due the presence of ‘max’ function.

    • The set of \(|S|\) equations for \(\pi^*(s)\) cannot be solved directly as it is dependent on unknown \(U^*(s)\).

Optimal Policy for MDP

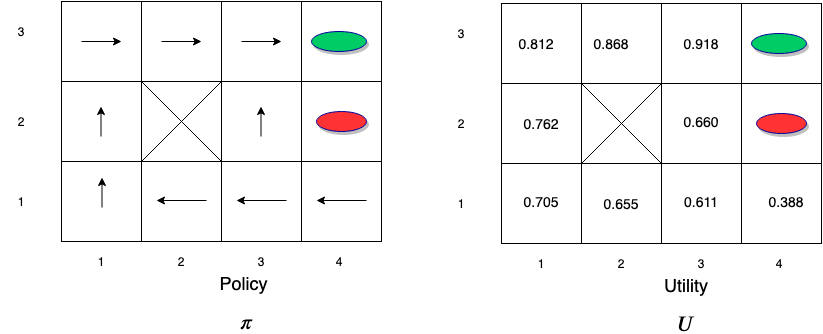
Optimal Policy and Utilities for Maze

Value Iteration

  • To solve the non-linear equations for \(U^{*}(s)\) we use an iterative approach.
  • Steps:
    • Initialize estimates for the utilities of states with arbitrary values: \(U(s) \leftarrow 0 \forall s \epsilon S\)
    • Next use the iteration step below which is also called Bellman Update:

\[V_{t+1}(s) \leftarrow R(s) + \gamma \underset{a}{ \max} \left[ \sum_{s^{'}} P(s^{'}| s,a) U_t(s^{'}) \right] \forall s \epsilon S\]

This step is repeated and updated
  • Let us apply this to the maze example. Assume that \(\gamma = 1\)

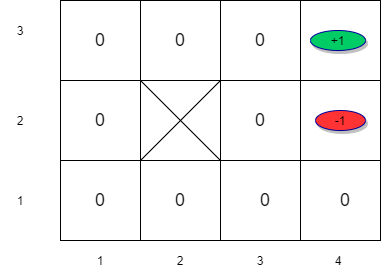val-iter-initial Initialize value estimates to \(0\)

Value Iteration

  • Next we want to apply Bellman Update: \[V_{t+1}(s) \leftarrow R(s) + \gamma \max_{a} \left[\sum_{s^\prime} P(s^\prime | s,a)U_t(s^\prime) \right] \forall s \epsilon S\]
  • Since we are taking \(\max\) we only need to consider states whose next states have a positive utility value.
  • For the remaining states, the utility is equal to the immediate reward in the first iteration.

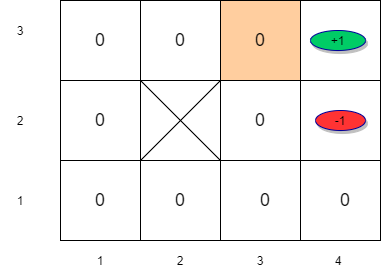
States to consider for value iteration

Value Iteration (t=0)

\[ V_{t+1}(s_{33}) = R(s_{33}) + \gamma \max_a \left[\sum_{s^{'}} P(s^{'}| s_{33},a)U(s^{'}) \right] \forall s \in S \]

\[ V_{t+1}(s_{33}) = -0.04 + \max_a \left[ \sum_{s'} P(s'| s_{33},\uparrow) U_t(s'), \sum_{s'} P(s'| s_{33},\downarrow)U_t(s'), \sum_{s'} P(s'| s_{33},\rightarrow) U_t(s'), \sum_{s'} P(s'| s_{33}, \leftarrow)U_t(s') \right]\]

\[V_{t+1}(s_{33}) = -0.04 + \sum_{s^{'}} P(s^{'}| s_{33},\rightarrow) U_t(s^\prime) \]

\[V_{t+1}(s_{33}) = -0.04 + P(s_{43}|s_{33},\rightarrow)U(s_{43})+P(s_{33}|s_{33},\rightarrow)U(s_{33})+P(s_{32}|s_{33},\rightarrow)U_t(s_{32}) \]

\[V_{t+1}(s_{33}) = -0.04 + 0.8 \times 1 + 0.1 \times 0 + 0.1 \times 0 = 0.76 \]

Value Iteration (t=1)

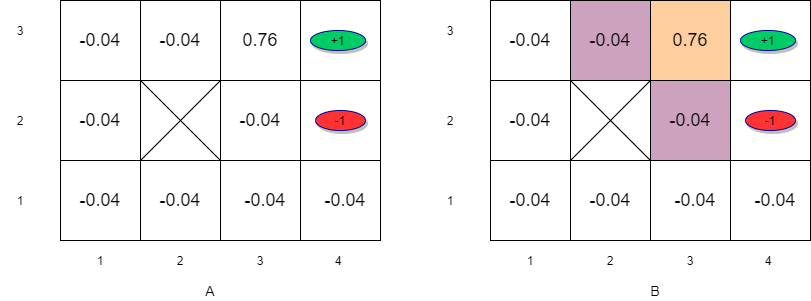val-iter-step2 (A) Initial utility estimates for iteration 2. (B) States with next state positive utility

\[V_{t+1}(s_{33}) = -0.04 + P(s_{43}|s_{33},\rightarrow)U_t(s_{43})+P(s_{33}|s_{33},\rightarrow)U_t(s_{33}) +P(s_{32}|s_{33},\rightarrow)U_t(s_{32}) \]

\[V_{t+1}(s_{33}) = -0.04 + 0.8 \times 1 + 0.1 \times 0.76 + 0.1 \times 0 = 0.836\]

\[V_{t+1}(s_{23}) = -0.04 + P(s_{33}|s_{23},\rightarrow)U_t(s_{23})+P(s_{23}|s_{23},\rightarrow)U_t(s_{23}) = -0.04 + 0.8 \times 0.76 = 0.568\]

\[V_{t+1}(s_{32}) = -0.04 + P(s_{33}|s_{32},\uparrow)U_t(s_{33})+P(s_{42}|s_{32},\uparrow)U_t(s_{42}) +P(s_{32}|s_{32},\uparrow)U_t(s_{32})\] \[V_{t+1}(s_{32}) = -0.04 + 0.8 \times 0.76 + 0.1 \times -1 + 0.1 \times 0= 0.468\]

Value Iteration (t=2)

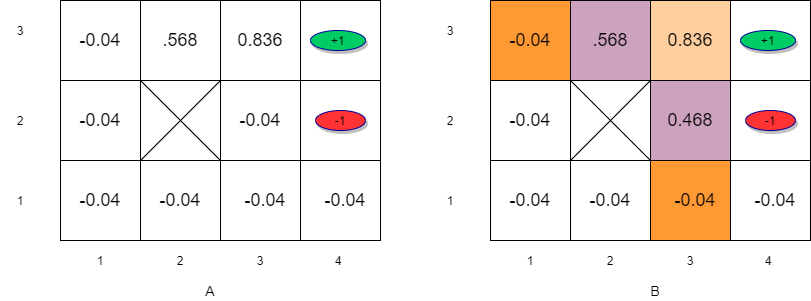val-iter-step3 (A)Initial utility estimates for iteration 3. (B) States with next state positive utility

  • Information propagates outward from terminal states and eventually all states have correct value estimates
  • Notice that \(s_{32}\) has a lower utility compared to \(s_{23}\) due to the red oval state with negative reward next to \(s_{32}\)

Optimal Policy and Utilities for Maze

Value Iteration - Convergence

  • Rate of convergence depends on the maximum reward value and more importantly on the discount factor \(\gamma\).
  • The policy that we get from coarse estimates is close to the optimal policy long before \(U\) has converged.
  • This means that after a reasonable number of iterations, we could use: \[\pi(s) = \arg \max_a \left[ \sum_{s^{'}} P(s^{'}| s,a)V_{est}(s^{'}) \right]\]
  • Note that this is a form of greedy policy.

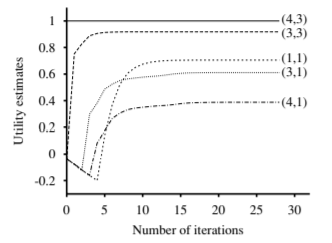
value-iter-convergence Convergence of utility for the maze problem (Norvig chap 17)

  • For the maze problem, convergence is reached within 5 to 10 iterations

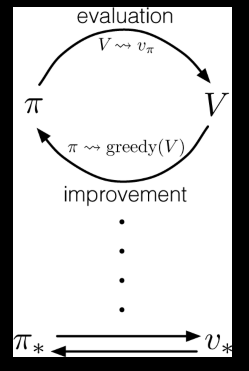
Policy Iteration

  • Alternates between two steps:

    • Policy evaluation: given a policy, find the utility of states
    • Policy improvement: given the utility estimates so far, find the best policy

  • The steps are as follows:

    1. Compute utility/value of the policy \(U^{\pi}\)
    2. Update \(\pi\) to be a greedy policy w.r.t. \(U^{\pi}\): \[\pi(s) \leftarrow \arg\max_a \sum_{s^\prime} P(s^\prime|s,a)U^{\pi}(s^\prime)\]
    3. If the policy changed then return to step \(1\)

  • Policy improves each step and converges to the optimal policy \(\pi^{*}\)

Policy iteration(source: sutton, chap 4)

Back to top