R = rot2(0.3)array([[ 0.9553, -0.2955],
[ 0.2955, 0.9553]])Robotics, Vision & Control 3e: for Python
Copyright (c) 2021- Peter Corke
There are some minor code changes compared to the book. These are to support the Matplotlib widget (ipympl) backend. This allows 3D plots to be rotated so the changes are worthwhile.
\(\displaystyle \left[\begin{matrix}\cos{\left(\theta \right)} & - \sin{\left(\theta \right)}\\\sin{\left(\theta \right)} & \cos{\left(\theta \right)}\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}\cos{\left(2 \theta \right)} & - \sin{\left(2 \theta \right)}\\\sin{\left(2 \theta \right)} & \cos{\left(2 \theta \right)}\end{matrix}\right]\)
plotvol2([0, 5], new=True) # new plot with both axes from 0 to 5
trplot2(TA, frame="A", color="b")
T0 = transl2(0, 0)
trplot2(T0, frame="0", color="k") # reference frame
TB = transl2(2, 1)
trplot2(TB, frame="B", color="r")
TAB = TA @ TB
trplot2(TAB, frame="AB", color="g")
TBA = TB @ TA
trplot2(TBA, frame="BA", color="c")
P = np.array([3, 2])
plot_point(P, "ko", label="P");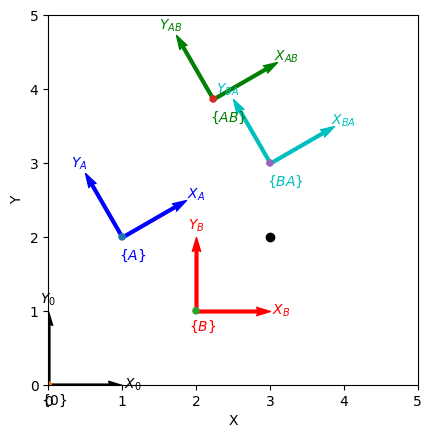
[[ 0.866 -0.5 1]
[ 0.5 0.866 2]
[ 0 0 1]]
[3 2]array([ 1.732, -1, 1])plotvol2([-5, 4, -1, 5], new=True) # for matplotlib/widget
T0 = transl2(0, 0)
trplot2(T0, frame="0", color="k")
TX = transl2(2, 3)
trplot2(TX, frame="X", color="b")
TR = trot2(2)
trplot2(TR @ TX, framelabel="RX", color="g")
trplot2(TX @ TR, framelabel="XR", color="g")
C = np.array([3, 2])
plot_point(C, "ko", text="C")
TC = transl2(C) @ TR @ transl2(-C)
trplot2(TC @ TX, framelabel="XC", color="r");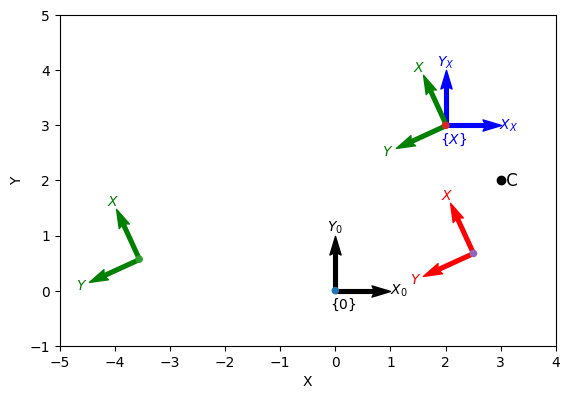
array([[ -0.4161, -0.9093, 6.067],
[ 0.9093, -0.4161, 0.1044],
[ 0, 0, 1]])import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
from scipy.linalg import logm, expm
import tempfile
import os
from IPython.display import Image, display
def create_rotation_gif(R, filename=None, frames=60, duration=3.0, figsize=(8, 6), dpi=100):
"""
Create GIF animation of 3D coordinate frame rotation
Parameters:
- R: 3x3 rotation matrix
- filename: output filename (optional, creates temp file if None)
- frames: number of animation frames
- duration: animation duration in seconds
- figsize: figure size tuple
- dpi: dots per inch for output quality
Returns:
- filename of created GIF or IPython Image object
"""
fig = plt.figure(figsize=figsize, dpi=dpi)
ax = fig.add_subplot(111, projection="3d")
# Generate smooth rotation sequence
angles = np.linspace(0, 1, frames)
# Create rotation interpolation
if np.allclose(R, np.eye(3)):
# If identity matrix, create a full rotation for visualization
R_seq = [expm(t * 2 * np.pi * np.array([[0, -1, 0], [1, 0, 0], [0, 0, 0]])) for t in angles]
else:
# Interpolate to the target rotation
try:
log_R = logm(R)
R_seq = [expm(t * log_R) for t in angles]
except:
# Fallback for problematic matrices
R_seq = [R for _ in angles]
def animate_frame(frame_idx):
ax.clear()
ax.set_xlim([-1.2, 1.2])
ax.set_ylim([-1.2, 1.2])
ax.set_zlim([-1.2, 1.2])
R_current = R_seq[frame_idx]
origin = [0, 0, 0]
# Draw reference coordinate frame (fixed, gray)
ax.quiver(
*origin,
1,
0,
0,
color="lightgray",
arrow_length_ratio=0.1,
linewidth=1,
alpha=0.5,
)
ax.quiver(
*origin,
0,
1,
0,
color="lightgray",
arrow_length_ratio=0.1,
linewidth=1,
alpha=0.5,
)
ax.quiver(
*origin,
0,
0,
1,
color="lightgray",
arrow_length_ratio=0.1,
linewidth=1,
alpha=0.5,
)
# Draw animated coordinate axes with proper colors and labels
# X-axis (red)
ax.quiver(
*origin,
R_current[0, 0],
R_current[1, 0],
R_current[2, 0],
color="red",
arrow_length_ratio=0.1,
linewidth=3,
)
ax.text(
R_current[0, 0] * 1.3,
R_current[1, 0] * 1.3,
R_current[2, 0] * 1.3,
"X",
color="red",
fontsize=12,
fontweight="bold",
)
# Y-axis (green)
ax.quiver(
*origin,
R_current[0, 1],
R_current[1, 1],
R_current[2, 1],
color="green",
arrow_length_ratio=0.1,
linewidth=3,
)
ax.text(
R_current[0, 1] * 1.3,
R_current[1, 1] * 1.3,
R_current[2, 1] * 1.3,
"Y",
color="green",
fontsize=12,
fontweight="bold",
)
# Z-axis (blue)
ax.quiver(
*origin,
R_current[0, 2],
R_current[1, 2],
R_current[2, 2],
color="blue",
arrow_length_ratio=0.1,
linewidth=3,
)
ax.text(
R_current[0, 2] * 1.3,
R_current[1, 2] * 1.3,
R_current[2, 2] * 1.3,
"Z",
color="blue",
fontsize=12,
fontweight="bold",
)
# Set labels and title
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.set_title(f"Coordinate Frame Animation\nFrame {frame_idx + 1}/{frames}")
# Keep camera view fixed for better visualization of rotation
ax.view_init(elev=20, azim=45)
# Create animation
anim = animation.FuncAnimation(
fig,
animate_frame,
frames=frames,
interval=duration * 1000 / frames,
repeat=True,
)
# Save as GIF using Pillow writer (more reliable than ffmpeg)
if filename is None:
with tempfile.NamedTemporaryFile(suffix=".gif", delete=False) as tmp:
filename = tmp.name
# Save with Pillow writer
writer = animation.PillowWriter(fps=frames / duration)
anim.save(filename, writer=writer)
plt.close(fig)
# Read and return as IPython Image for Jupyter display
with open(filename, "rb") as f:
gif_data = f.read()
# Clean up temporary file
os.unlink(filename)
return Image(data=gif_data, format="gif")
else:
# Save to specified file
writer = animation.PillowWriter(fps=frames / duration)
anim.save(filename, writer=writer)
plt.close(fig)
return filename
def tranimate_gif(R, save_path=None, **kwargs):
"""
GIF-based replacement for tranimate function
Parameters:
- R: rotation matrix
- save_path: optional path to save GIF
- **kwargs: additional animation parameters
Returns:
- IPython Image object for Jupyter display or filename if saved
"""
return create_rotation_gif(R, filename=save_path, **kwargs)# Replace the problematic cell with:
# ...existing code...
# from spatialmath.base.gif_animate import tranimate_gif
R = rotx(pi / 2)
# Create and display GIF animation instead of HTML5 video
gif_animation = tranimate_gif(R, frames=60, duration=3.0)
display(gif_animation)
# Optional: Save the animation for use in documentation
# tranimate_gif(R, save_path="figures/rotation_x_90deg.gif")<IPython.core.display.Image object>Robust, portable animation in Jupyter notebooks is challenging. We’ve replaced the original tranimate HTML5 video animations with a custom GIF-based animation function for better compatibility:
gif_animation = tranimate_gif(R, frames=60, duration=3.0)
display(gif_animation)If you wish to animate a coordinate frame from a regular Python script, you can still use the simpler syntax:
tranimate(R)array([[ 0.9021, -0.3836, 0.1977],
[ 0.3875, 0.9216, 0.01983],
[ -0.1898, 0.05871, 0.9801]])array([[ 0.9021, -0.3836, -0.1977],
[ 0.3875, 0.9216, -0.01983],
[ 0.1898, -0.05871, 0.9801]])array([[ 0.9021, -0.3836, -0.1977],
[ 0.3875, 0.9216, -0.01983],
[ 0.1898, -0.05871, 0.9801]])array([[ 0.9363, -0.2751, 0.2184],
[ 0.2896, 0.9564, -0.03696],
[ -0.1987, 0.09784, 0.9752]])array([[ 0.9752, -0.09784, 0.1987],
[ 0.1538, 0.9447, -0.2896],
[ -0.1593, 0.313, 0.9363]])The next cell will launch an interactive tool (using the Swift visualizer) in a new browser tab. Close the browser tab when you are done with it.
You might also have to stop the cell from executing, by pressing the stop button for the cell. It may terminate with lots of errors, don’t panic.
array([[ 0.69442042+0.j , 0.69442042-0.j , 0.18857511+0.j ],
[-0.07921035-0.56882404j, -0.07921035+0.56882404j, 0.58337798+0.j ],
[-0.10726605+0.42004668j, -0.10726605-0.42004668j, 0.79000605+0.j ]])array([[ 1, 0, 0, 2],
[ 0, 0, -1, 0],
[ 0, 1, 0, 1],
[ 0, 0, 0, 1]])array([[ 1, 0, 0, 2],
[ 0, 0.9553, -0.2955, 3],
[ 0, 0.2955, 0.9553, 4],
[ 0, 0, 0, 1]])array([[ 1, 0, 0, 2],
[ 0, 0.9553, -0.2955, 3],
[ 0, 0.2955, 0.9553, 4],
[ 0, 0, 0, 1]])array([[ 0, -6, 5, 1],
[ 6, 0, -4, 2],
[ -5, 4, 0, 3],
[ 0, 0, 0, 0]])Axes3D(0.125,0.11;0.775x0.77)
(1.1204 1.6446 3.1778; 0.041006 0.4087 0.78907)array([[ 1, 0, 0, 0],
[ 0, 0.9553, -0.2955, 0],
[ 0, 0.2955, 0.9553, 0],
[ 0, 0, 0, 1]])Axes3D(0.125,0.11;0.775x0.77)
(1.1204 1.6446 3.1778; 0.041006 0.4087 0.78907)0.9029 -0.3796 0.2017 0.5447 0.3837 0.9232 0.01982 0.9153 -0.1937 0.05949 0.9793 1.542 0 0 0 1
NOTE
The next cell will launch an interactive tool (using the Swift visualizer) in a new browser tab. Close the browser tab when you are done with it.
You might also have to stop the cell from executing, by pressing the stop button for the cell. It may terminate with lots of errors, don’t panic.
spatialmath.pose3d.SO3 rpy/zyx = 17.2°, 0°, 0°