Rigid-body Motions
The general motion algebra introduced in robotics is implemented using a variety of motion representations, each suited to different modeling needs. Motion can be described using rotation matrices, axis-angle representations, quaternions, Euler angles, and other conventions.
The choice of representation depends on several factors. First, the domain in which the robot operates often dictates the preferred motion representation; for example, aeronautics and self-driving cars may use different conventions based on the types of robots employed or historical reasons. Second, robot vendors may publish their own conventions, as seen in resources like this explanation of robot orientation. Third, the tools used to implement algorithms may follow their own conventions, or may require translation between different representations during system integration.
Rigid-body motion in three-dimensional space requires an understanding of both position and orientation. A point in space is described by three coordinates, but a rigid body has six degrees of freedom: three for position and three for orientation.
In this context, rigid body configurations are encoded using 4×4 homogeneous transformation matrices. Orientation is represented by rotation matrices \(R \in SO(3)\). Spatial velocities are described by twists, which are six-dimensional vectors, and spatial forces are represented by wrenches, also six-dimensional vectors.
Vectors and Reference Frames
A vector \(\mathbf{v} \in \mathbb{R}^n\) is a geometric quantity that possesses both magnitude and direction. Vectors are inherently coordinate-free and only acquire specific numerical values when expressed in a particular coordinate frame. For example, a velocity vector may be \(\mathbf{v} = [3, 1, 0]^T\) in frame \(\{a\}\), but its representation will differ in another frame \(\{b\}\).
Points are also represented as vectors, with their coordinates defined relative to the origin of a reference frame as shown in Figure 1.
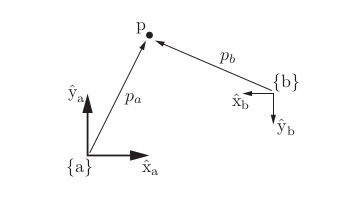
Suppose that a length scale and a fixed space reference frame {s} have been chosen as shown, with unit axes x̂s and ŷs . Similarly, we attach a reference frame with unit axes x̂b and ŷb to the planar body. Because this frame moves with the body, it is called the body frame and is denoted {b}. All frames discussed here are inertial. Even when referring to a “body frame,” the term means the inertial frame that instantaneously coincides with the moving frame.
Planar Rigid-Body Motions
In the plane, a rigid-body configuration is described by a rotation matrix \(P \in SO(2)\) and a translation vector \(\mathbf{p} \in \mathbb{R}^2\). Together, this pair \((P, \mathbf{p})\) allows us to represent the configuration of a body in the space frame, change the frame in which vectors are represented, and displace a point or frame through rotation and translation.
For example, consider a point \(q\) at \([1, 1]^T\) in a frame that is rotated 60° counterclockwise and translated by \([2, 1]^T\) as in Figure 2.
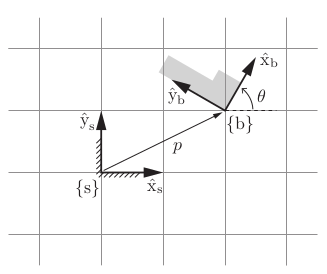
In the fixed frame, the transformation is given by:
\[ P = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}, \quad q' = Pq + \mathbf{p} \]
Although P consists of four numbers, they are subject to three constraints (each column of P must be a unit vector, and the two columns must be orthogonal to each other), and the one remaining degree of freedom is parametrized by θ. Together, the pair (P, p) provides a description of the orientation and position of {b} relative to {s}.
Any planar motion can also be interpreted as a rotation about a fixed point \(\mathbf{s}\). Lets look at planar motion of Figure 3.
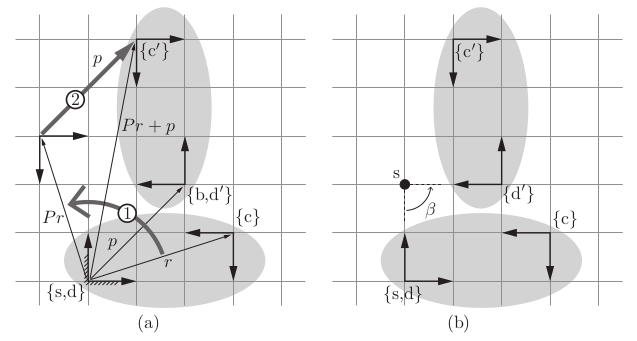
The frame {d}, fixed to an elliptical rigid body and initially coincident with {s}, is displaced to {d0 } (which is coincident with the stationary frame {b}), by first rotating according to P then translating according to p, where (P, p) is the representation of {b} in {s}. The same transformation takes the frame {c}, also attached to the rigid body, to {c0 }. The transformation marked 1 rigidly rotates {c} about the origin of {s}, and then transformation 2 translates the frame by p expressed in {s}.
Instead of viewing this displacement as a rotation followed by a translation, both rotation and translation can be performed simultaneously. The displacement can be viewed as a rotation of β = 90◦ about a fixed point s.
This is a planar example of a screw motion.1 The displacement can therefore be parametrized by the three screw coordinates \((β, s_x , s_y )\), where \((s_x , s_y ) = (0, 2)\) denotes the coordinates for the point s (i.e., the screw axis out of the page) in the fixed frame {s}.
Rotations and Angular Velocities in 3D
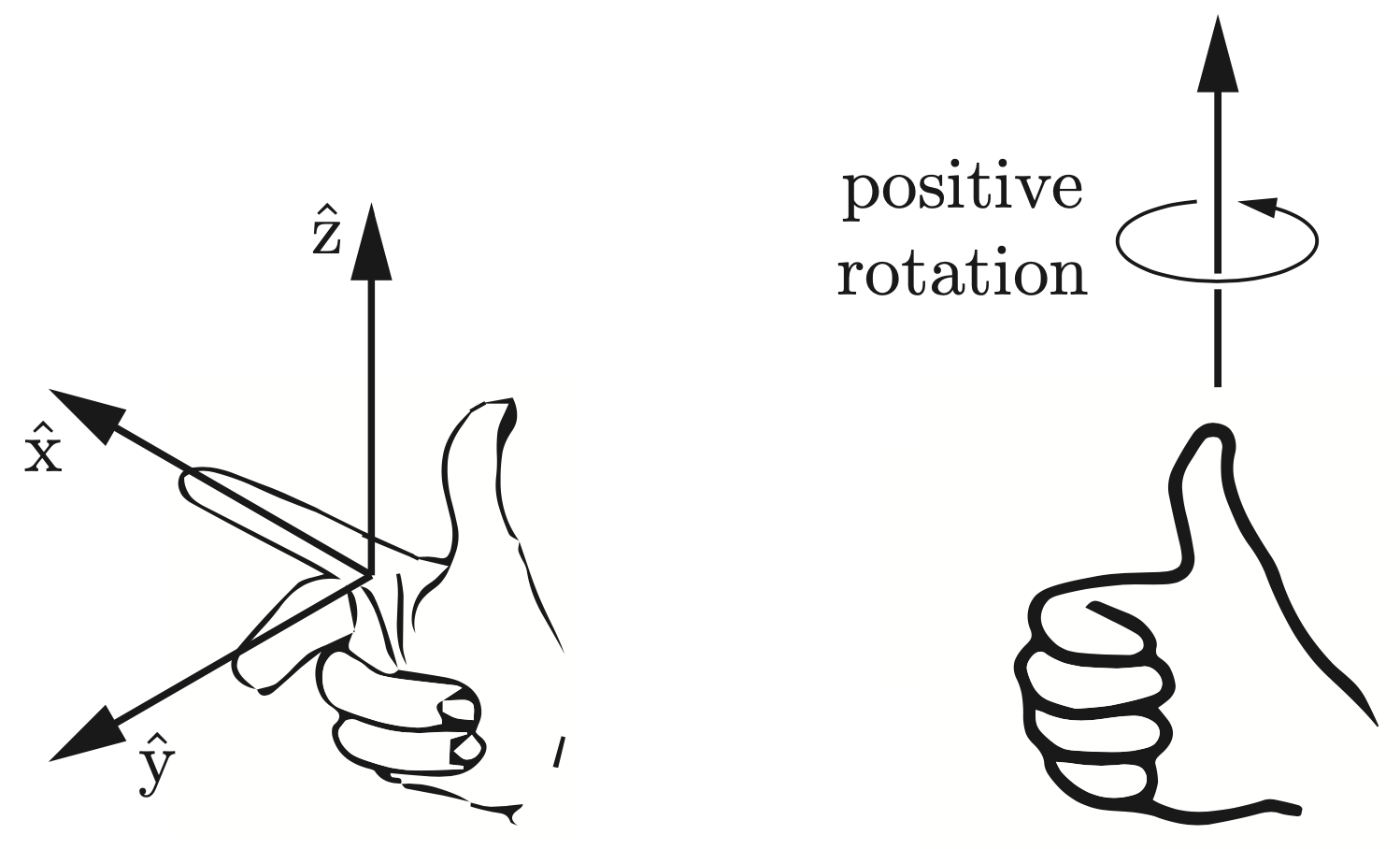
Lets expand now to the general 3D case as shown in Figure 4. By convention here all coordinate systems are right handed - a rule that is shown in Figure 5 and that where the unit axis satisfy \(\hat x \times \hat y = \hat z\).
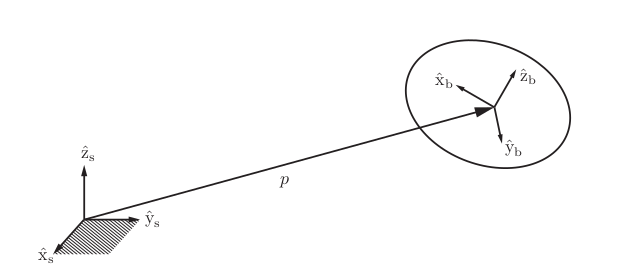
Let \(\mathbf{p}\) denote the vector from the fixed-frame origin to the body-frame origin. In terms of the fixed-frame coordinates, \(\mathbf{p}\) can be expressed as:
\[ \mathbf{p} = p_1 \, \hat{\mathbf{x}}_s + p_2 \, \hat{\mathbf{y}}_s + p_3 \, \hat{\mathbf{z}}_s \tag{3.12} \]
The axes of the body frame can also be expressed in the fixed frame as:
\[ \hat{\mathbf{x}}_b = r_{11} \hat{\mathbf{x}}_s + r_{21} \hat{\mathbf{y}}_s + r_{31} \hat{\mathbf{z}}_s \]
\[ \hat{\mathbf{y}}_b = r_{12} \hat{\mathbf{x}}_s + r_{22} \hat{\mathbf{y}}_s + r_{32} \hat{\mathbf{z}}_s \]
\[ \hat{\mathbf{z}}_b = r_{13} \hat{\mathbf{x}}_s + r_{23} \hat{\mathbf{y}}_s + r_{33} \hat{\mathbf{z}}_s \]
We now define the position vector \(\mathbf{p} \in \mathbb{R}^3\) and the rotation matrix \(R \in \mathbb{R}^{3 \times 3}\) as follows:
\[ \mathbf{p} = \begin{bmatrix} p_1 \\\\ p_2 \\\\ p_3 \end{bmatrix} \tag{3.13} \]
\[ R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\\\ r_{21} & r_{22} & r_{23} \\\\ r_{31} & r_{32} & r_{33} \end{bmatrix} = \left[ \hat{\mathbf{x}}_b \quad \hat{\mathbf{y}}_b \quad \hat{\mathbf{z}}_b \right] \tag{3.14–3.16} \]
The 12 parameters given by the pair \((R, \mathbf{p})\) provide a complete description of the position and orientation of the rigid body relative to the fixed frame.
The special orthogonal group \(SO(3)\), also known as the group of rotation matrices, is the set of all \(3 \times 3\) real matrices \(R\) that satisfy the following properties:
\[ R^T R = I \quad \text{and} \quad \det R = 1 \]
Some important properties of rotation matrices include: \(R^{-1} = R^T\), the composition of rotation matrices (\(R_1 R_2 \in SO(3)\)), and the preservation of vector lengths (\(\|Rv\| = \|v\|\)). Rotation matrices are used for representing orientation, changing coordinates, and rotating vectors.
SO(3) is a curved 3-dimensional space, but the feasible velocities at any point of SO(3) form a flat 3-dimensional vector space (the “tangent space”).
Angular Velocities
Suppose that a frame with unit axes \(\{\hat{x}, \hat{y}, \hat{z}\}\) is attached to a rotating body. Let us determine the time derivatives of these unit axes. Beginning with \(\hat{x}\), first note that \(\hat{x}\) is of unit length; only the direction of \(\hat{x}\) can vary with time (the same goes for \(\hat{y}\) and \(\hat{z}\)). If we examine the body frame at times \(t\) and \(t + \Delta t\), the change in frame orientation can be described as a rotation of angle \(\Delta \theta\) about some unit axis \(\hat{\mathbf \omega}\) passing through the origin. The axis \(\hat{w}\) is coordinate-free; it is not yet represented in any particular reference frame.
In the limit as \(\Delta t\) approaches zero, the ratio \(\Delta \theta / \Delta t\) becomes the rate of rotation \(\dot{\theta}\), and \(\hat{w}\) can similarly be regarded as the instantaneous axis of rotation.
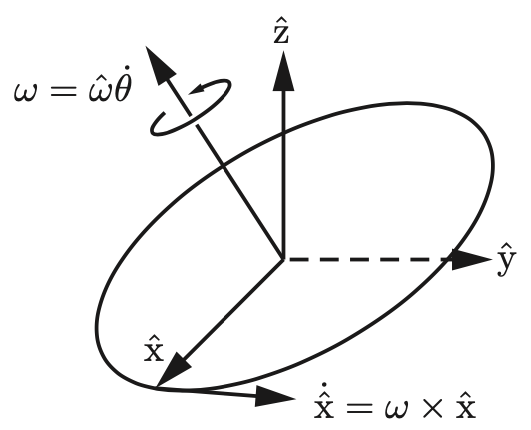
In fact as shown in Figure 6, \(\hat{\mathbf \omega}\) and \(\dot{\theta}\) can be combined to define the angular velocity \(\mathbf{\omega}\) as:
\[ \mathbf{\omega} = \hat{\mathbf \omega} \, \dot{\theta} \]
Let \(R(t)\) be the rotation matrix describing the orientation of the body frame with respect to the fixed frame at time \(t\); \(\dot{R}(t)\) is its time rate of change. The first column of \(R(t)\), denoted \(\mathbf{r}_1(t)\), describes \(\hat{x}\) in fixed-frame coordinates; similarly, \(\mathbf{r}_2(t)\) and \(\mathbf{r}_3(t)\) respectively describe \(\hat{y}\) and \(\hat{z}\) in fixed-frame coordinates. We can then write that
\[\dot r_i = \mathbf \omega_s \times r_i\]
where \(i=1,2,3\) and therefore
\[ \dot R = \mathbf \omega_s \times R\]
To eliminate the cross product on the right of the last expression, we introduce some new notation, rewriting \(\boldsymbol{\omega}_s \times R\) as \([\boldsymbol{\omega}_s] R\), where \([\boldsymbol{\omega}_s]\) is a \(3 \times 3\) skew- symmetric matrix representation of \(\boldsymbol{\omega}_s \in \mathbb{R}^3\).
Given a vector \(\mathbf{x} = [x_1\ x_2\ x_3]^T \in \mathbb{R}^3\), define
\[ [\mathbf{x}] = \begin{bmatrix} 0 & -x_3 & x_2 \\ x_3 & 0 & -x_1 \\ -x_2 & x_1 & 0 \end{bmatrix} \]
The matrix \([\mathbf{x}]\) is a \(3 \times 3\) skew-symmetric matrix representation of \(\mathbf{x}\); that is, \([\mathbf{x}] = -[\mathbf{x}]^T\).
The set of all \(3 \times 3\) real skew-symmetric matrices is called \(\mathfrak{so}(3)\).
It can be shown as in page 78 of Lynch and Park that the angular velocity can be described using rotation matrices: Given \(R(t)\), the spatial angular velocity is
\[[\omega_s] = R \dot{R}^T\]
and the body angular velocity is
\[[\omega_b] = R^T \dot{R}\].
The skew-symmetric matrix \([\omega]\) satisfies \([\omega]^T = -[\omega]^T\).
It is also important to note that the fixed-frame angular velocity \(\boldsymbol{\omega}_s\) does not depend on the choice of body frame. Similarly, the body-frame angular velocity \(\boldsymbol{\omega}_b\) does not depend on the choice of fixed frame. While these equations may appear to depend on both frames (since \(R\) and \(\dot{R}\) individually depend on both \(\{s\}\) and \(\{b\}\)), the product \(\dot{R} R^{-1}\) is independent of \(\{b\}\) and the product \(R^{-1} \dot{R}\) is independent of \(\{s\}\).
Exponential Coordinate Representation of Rotations
Rodrigues’ formula provides a way to compute rotation matrices:
\[ R = I + \sin\theta [\omega] + (1 - \cos\theta)[\omega]^2 \]
This formula defines the exponential coordinates of rotation. Any rotation can be expressed as:
\[ R = e^{[\omega]\theta} \]

The logarithm of a rotation is the inverse of the matrix exponential. If \(\theta \neq 0\), then:
\[ [\omega] = \frac{1}{2 \sin \theta}(R - R^T) \]
Rigid-Body Motions in SE(3)
Rigid-body motions in three-dimensional space are described using homogeneous transformation matrices:
\[ T = \begin{bmatrix} R & \mathbf{p} \\ 0 & 1 \end{bmatrix} \in SE(3) \]
This matrix encodes both rotation and translation. The inverse of a homogeneous transformation matrix is given by:
\[ T^{-1} = \begin{bmatrix} R^T & -R^T \mathbf{p} \\ 0 & 1 \end{bmatrix} \]
Composing transformations is straightforward:
\[ T_{ac} = T_{ab} T_{bc} \]
Twists (Spatial Velocities)
A twist is a six-dimensional vector that combines angular and linear velocity:
\[ V = \begin{bmatrix} \omega \\ v \end{bmatrix} \in \mathbb{R}^6 \]
The matrix representation of a twist is:
\[ [V] = \begin{bmatrix} [\omega] & v \\ 0 & 0 \end{bmatrix} \in \mathfrak{se}(3) \]
Body and spatial twists are defined as follows: \([V_b] = T^{-1} \dot{T}\) and \([V_s] = \dot{T} T^{-1}\).
The adjoint operator is given by:
\[ \text{Ad}_T = \begin{bmatrix} R & 0 \\ [\mathbf{p}]R & R \end{bmatrix}, \quad V_s = \text{Ad}_T V_b \]
Exponential Coordinates for Rigid Motions
Exponential coordinates provide a compact way to describe rigid motions. Let \(S = (\omega, v) \in \mathbb{R}^6\) be a screw axis. The transformation is given by:
\[ e^{[S]\theta} = \begin{bmatrix} e^{[\omega]\theta} & G(\theta)v \\ 0 & 1 \end{bmatrix} \]
where
\[ G(\theta) = I\theta + (1 - \cos\theta)[\omega] + (\theta - \sin\theta)[\omega]^2 \]
Given a transformation \(T = (R, \mathbf{p})\), the matrix logarithm is used as follows:
\(\log R \rightarrow [\omega]\theta\)
\(v = G(\theta)^{-1} \mathbf{p}\)
Thus, \([S]\theta = \log T\).
Wrenches (Spatial Forces)
A wrench is a six-dimensional vector that combines force and torque:
\[ F = \begin{bmatrix} \tau \\ f \end{bmatrix} \]
Here, \(f\) is the force and \(\tau = r \times f\) is the torque (moment).
Coordinate transformations for wrenches are given by:
\[ F_b = \text{Ad}_T^T F_a \]
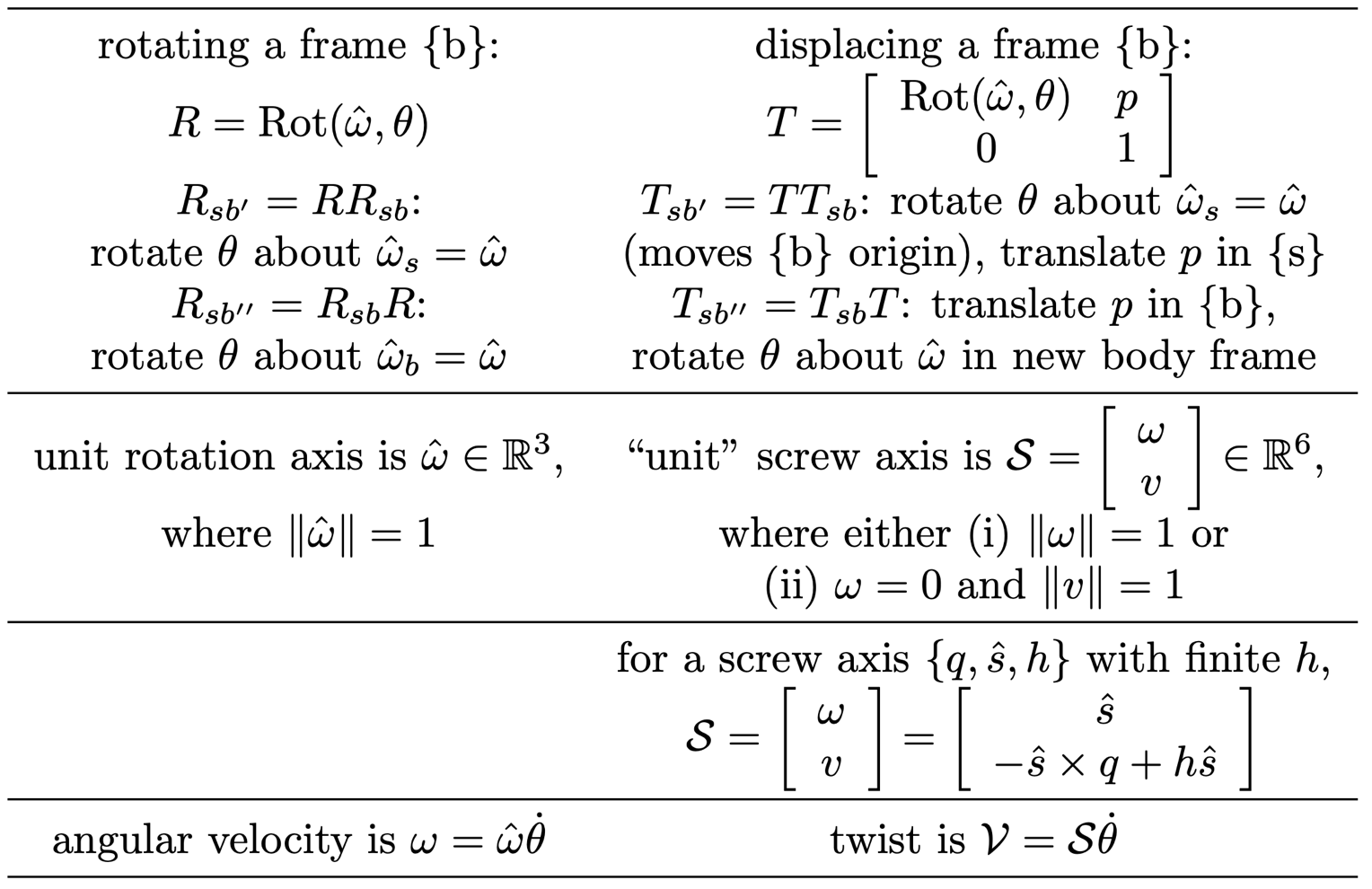
Summary of rotation and motion representations



Other representations
This section borrows heavily from the book Introduction to Autonomous Robots.
Euler Angles
In fact, three values are sufficient to describe orientation. This becomes clear when considering that orthogonality (dot product of all columns is zero) and vector length (each vector must have length 1) impose six constraints on the nine values in the rotation matrix. Indeed, an orientation can be represented as a rotation by certain angles around the \(x\), the \(y\), and the \(z\)-axis of the reference coordinate system. This is known as the X-Y-Z fixed-angle notation. Mathematically, this can be represented by a rotation matrix of the form:
\[^s_BR_{XYZ}(\gamma,\beta,\alpha)=\begin{bsmallmatrix}\cos\alpha & -\sin\alpha & 0\\ \sin\alpha & \cos\alpha & 0\\0 & 0 & 1\end{bsmallmatrix}\begin{bsmallmatrix}cos\beta& 0 & \sin\beta\\0 & 1 & 0\\-\sin\beta & 0 & \cos\beta\end{bsmallmatrix}\begin{bsmallmatrix}1 & 0 & 0 \\ 0 & \cos\gamma & -\sin\gamma\\0 & \sin\gamma & \cos\gamma\end{bsmallmatrix}\]
While the X-Y-Z fixed angles approach expresses a coordinate frame using rotations with respect to the original coordinate frame (say, \(\{A\}\)), another possible description is to start with a coordinate frame \(\{B\}\) that is coincident with frame \(\{A\}\), then rotate around the Z-axis with angle \(\alpha\), then the Y-axis with angle \(\beta\) and finally around the X-axis with angle \(\gamma\). This representation is called Z-Y-X Euler angles.
As the coordinate axis do not necessarily need to be different, there are twelve possible valid combinations of sub-sequent rotations: XYX, XZX, YXY, YZY, ZXZ, ZYZ, XYZ, XZY, YZX, YXZ, ZXY and ZYX. The reason for which there are only twelve is that sub-sequent rotations around the same axis are not valid. Such rotations would not add any information, but are equivalent to a rotation by the sum of both angles.
It is important to understand the subtle differences between the available transformations as there is neither “right” nor “wrong” convention, however different manufacturers of hardware and software products might use different ones, often based on preferences in the various different fields, such as aviation or geology, that these algorithms and products originally catered to.
There is a fundamental caveat with all of the above approaches: each of the rotation matrices can look like subsequent rotations around the same axis for certain values of angles. For example, this happens for the XYZ rotation matrix if the angle of rotation around the Y-axis is 90°. These cases are known as a singularities of the specific notation. We therefore need additional representations that work across the entire range of possible motions.
Quaternions
Among the many possible conventions, the preferred representation for computational and stability reasons are quaternions. A quaternion is a 4-tuple that extends the complex numbers with very general applications in mathematics and representing orientation and rotation in particular. Quaternions are generally represented in the form
\[q=a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}\]
Here, \(a\) is referred to the scalar part of the Quaternion and the elements \(b\), \(c\) and \(d\) as the vector part.
A Quaternion’s conjugate is given by
\[q^*=a-b\mathbf{i}-c\mathbf{j}-d\mathbf{k}\]
It can be shown that that each rotation can be represented as a rotation around a single axis (a vector in space) by a specific angle, also known as Euler axis. Given such an axis \(\hat{K}=[k_x k_y k_z]^T\) and an angle \(\theta\), one can calculate the so-called Euler parameters or unit quaternion \(\mathbf{q}=(\epsilon_1,\epsilon_2,\epsilon_3,\epsilon_4)\) with
\[\begin{align} \epsilon_1&=\cos \frac{\theta}{2}\\ \epsilon_2&=k_x \sin \frac{\theta}{2}\\ \epsilon_3&=k_y \sin \frac{\theta}{2}\\ \epsilon_4&=k_z \sin\frac{\theta}{2} \end{align}\]
These four quantities are constrained by the relationship
\[\epsilon_1^2+\epsilon_2^2+\epsilon_3^2+\epsilon_4^2=1\]
which might be visualized by a point on a unit hyper-sphere.
Given a vector \(\mathbf{p} \in \mathbb{R}^3\) that should be rotated by a unit Quaternion \(\mathbf{q}\), we can compute the new vector \(\mathbf{p'}\) as
\[\mathbf{p'}=\mathbf{q}\mathbf{p}\mathbf{q^*}\]
with \(\mathbf{q^*}\) the conjugate of \(\mathbf{q}\) as defined above.
Computing the equivalent rotation to two subsequent rotations, requires multiplying the Quaternions. Given two quaternions \(\epsilon\) and \(\epsilon'\), multiplication is defined by the following matrix multiplication:
\[\left[\begin{array}{cccc} \epsilon_4 & \epsilon_1 & \epsilon_2 & \epsilon_3\\ -\epsilon_1 & \epsilon_4 & -\epsilon_3 & \epsilon_2\\ -\epsilon_2 & \epsilon_3 & \epsilon_4 & -\epsilon_1\\ -\epsilon_3 & -\epsilon_2 & \epsilon_1 & \epsilon_4 \end{array}\right] \left[\begin{array}{c}\epsilon_4'\\\epsilon_1'\\\epsilon_2'\\\epsilon_3'\end{array}\right]\]
Unlike multiplying two rotation matrices, which requires 27 multiplications and 18 additions, multiplying two quaternions only requires 16 multiplications and 12 additions, making the operation computationally more efficient. Importantly, this representation does not suffer from singularities for specific joint angles, making the approach computationally more robust. This is particularly relevant for robotics, as singularities have pretty significant real-world impact on physical robots.
References
Lynch and Park, Modern Robotics: Mechanics, Planning, and Control (2017)