Pinhole Camera Model

Figure 1: Pinhole camera model. The image is formed on the image plane by light rays passing through a small aperture (the pinhole) at the center of projection. The image is inverted and smaller than the object.

Camera Model Fundamentals

Pinhole Camera Model

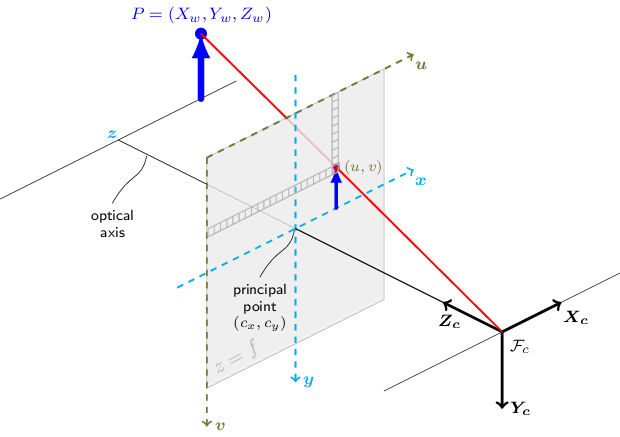
The functions in this section use a so-called pinhole camera model. The view of a scene is obtained by projecting a scene’s 3D point \(P_w\) into the image plane using a perspective transformation which forms the corresponding pixel \(p\). Both \(P_w\) and \(p\) are represented in homogeneous coordinates, i.e. as 3D and 2D homogeneous vector respectively.

The distortion-free projective transformation given by a pinhole camera model is:

\[\lambda \; p = K \begin{bmatrix} R|t \end{bmatrix} P_w\]

where:

  • \(P_w\) is a 3D point expressed with respect to the world coordinate system

  • \(p\) is a 2D pixel in the image plane

  • \(K\) is the camera intrinsic matrix

  • \(R\) and \(t\) are the rotation and translation that describe the change of coordinates from world to camera coordinate systems

  • \(\lambda\) is the projective transformation’s arbitrary scaling

Camera Intrinsic Matrix

The camera intrinsic matrix \(K\)projects 3D points given in the camera coordinate system to 2D pixel coordinates:

\[p = K P_c\]

The camera intrinsic matrix \(K\) is composed of the focal lengths \(f_x\) and \(f_y\), which are expressed in pixel units, and the principal point \((c_x, c_y)\), that is usually close to the image center:

\[K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}\]

and thus:

\[\lambda \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix}\]

Coordinate Transformations

The joint rotation-translation matrix \([R|t]\) is the matrix product of a projective transformation and a homogeneous transformation. The 3-by-4 projective transformation maps 3D points represented in camera coordinates to 2D points in the image plane and represented in normalized camera coordinates \(x' = X_c / Z_c\) and \(y' = Y_c / Z_c\).

The homogeneous transformation is encoded by the extrinsic parameters \(R\) and \(t\) and represents the change of basis from world coordinate system \(w\) to the camera coordinate system \(c\):

\[P_c = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} P_w\]

This gives us the complete transformation:

\[\lambda \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}\]

If \(Z_c \neq 0\), this is equivalent to:

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x X_c/Z_c + c_x \\ f_y Y_c/Z_c + c_y \end{bmatrix}\]

Lens Distortion Model

Real lenses introduce distortions (radial and tangential).

Figure 2: Distortion examples: barrel, pincushion, and tangential distortions.

The extended camera model accounts for this:

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x x'' + c_x \\ f_y y'' + c_y \end{bmatrix}\]

where:

\[\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} x' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + 2 p_1 x' y' + p_2(r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4 \\ y' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \end{bmatrix}\]

with \(r^2 = x'^2 + y'^2\) and \(\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} X_c/Z_c \\ Y_c/Z_c \end{bmatrix}\) if \(Z_c \neq 0\).

Distortion Parameters:

  • Radial coefficients: \(k_1\), \(k_2\), \(k_3\), \(k_4\), \(k_5\), \(k_6\)

  • Tangential coefficients: \(p_1\), \(p_2\)

  • Thin prism coefficients: \(s_1\), \(s_2\), \(s_3\), \(s_4\)

The distortion coefficients are passed as:

\[(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\]

Types of Distortion:

  • Barrel distortion: \((1 + k_1 r^2 + k_2 r^4 + k_3 r^6)\) monotonically decreasing

  • Pincushion distortion: \((1 + k_1 r^2 + k_2 r^4 + k_3 r^6)\) monotonically increasing

Right handed vs Left-handed coordinate systems

The right handed and left-handed coordinate systems are two conventions for defining the orientation of axes in 3D space. Some applications prefer one over the other, and it is important to be aware of which one you are using.

ROS2

The table below shows what ROS2 RViz2 displays - its a right handed coordinate system. The right hand rule is used to determine the direction of the axes: if you point your thumb in the direction of the X-axis, your index finger in the direction of the Y-axis, then your middle finger will point in the direction of the Z-axis.

Axis Direction Color
X Forward 🔴 Red
Y Left 🟢 Green
Z Up 🔵 Blue

Sensor Coordinate Systems

Each sensor has its own coordinate system, supported by the vendor documentation , which may be right-handed or left-handed. Take for example RealSense cameras - a real-handed sensor.

::: {.callout-note title: RealSense and ROS2}

  • Point Of View:
    • Imagine we are standing behind of the camera, and looking forward.
    • Always use this point of view when talking about coordinates, left vs right IRs, position of sensor, etc..

image
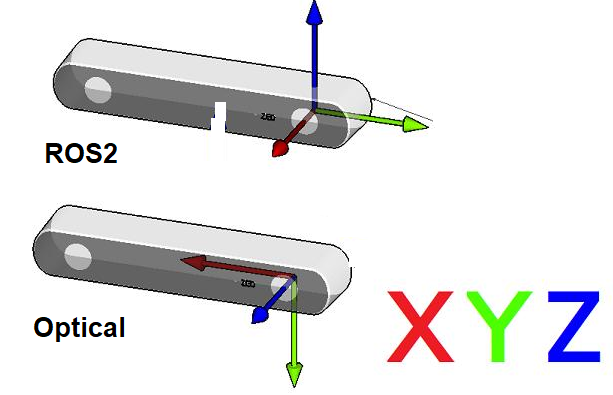
  • ROS2 Coordinate System: (X: Forward, Y:Left, Z: Up)
  • Camera Optical Coordinate System: (X: Right, Y: Down, Z: Forward)
  • References: REP-0103, REP-0105
  • All data published in our wrapper topics is optical data taken directly from our camera sensors.
  • static and dynamic TF topics publish optical CS and ROS CS to give the user the ability to move from one CS to other CS.

TF from coordinate A to coordinate B:

  • TF msg expresses a transform from coordinate frame “header.frame_id” (source) to the coordinate frame child_frame_id (destination) Reference
  • In RealSense cameras, the origin point (0,0,0) is taken from the left IR (infra1) position and named as “camera_link” frame
  • Depth, left IR and “camera_link” coordinates converge together.
  • Our wrapper provide static TFs between each sensor coordinate to the camera base (camera_link)
  • Also, it provides TFs from each sensor ROS coordinates to its corrosponding optical coordinates.
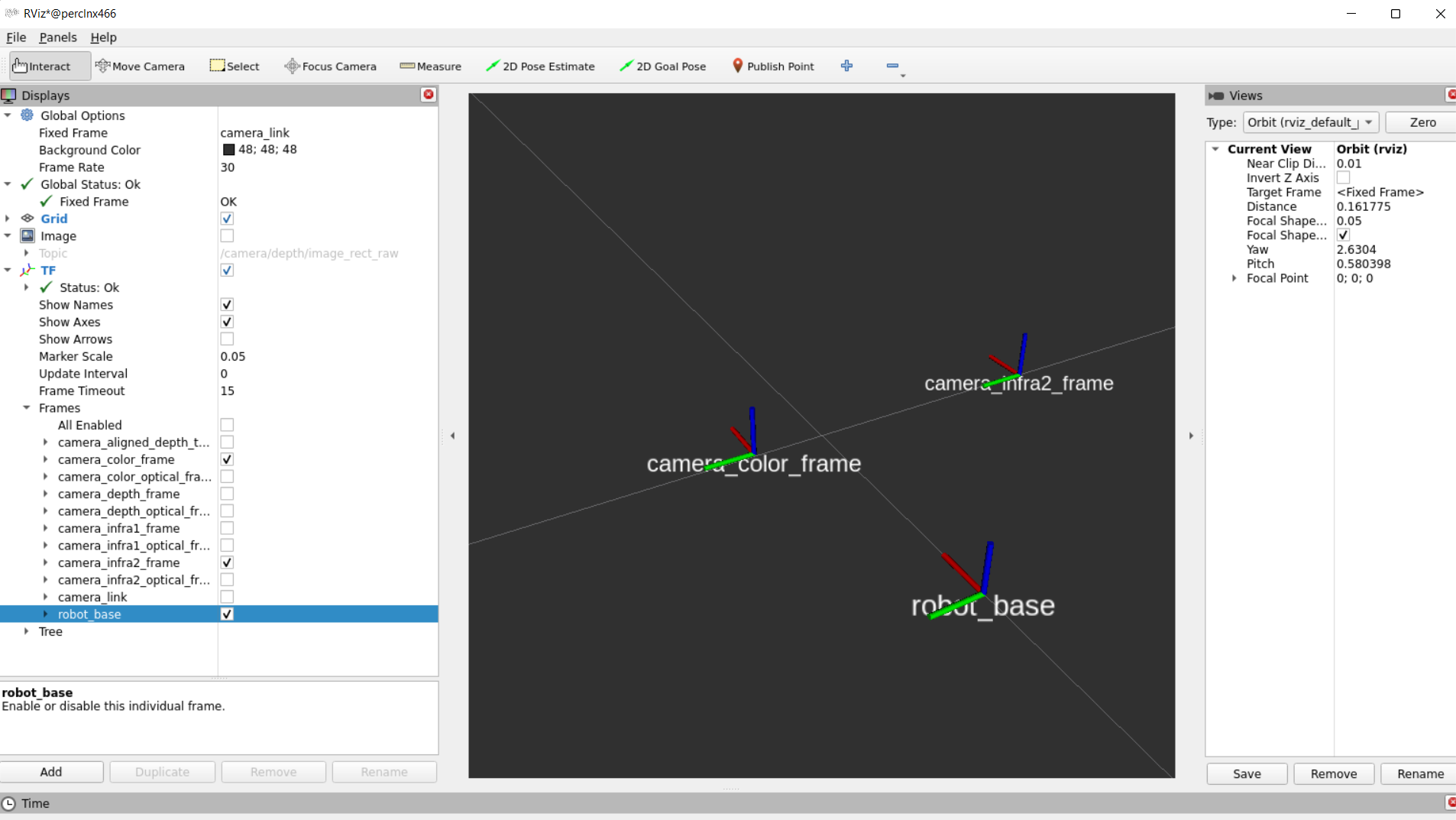
  • Example of static TFs of RGB sensor and Infra2 (right infra) sensor of D435i module as it shown in rviz2: example

Extrinsics from sensor A to sensor B:

  • Extrinsic from sensor A to sensor B means the position and orientation of sensor A relative to sensor B.
  • Imagine that B is the origin (0,0,0), then the Extrensics(A->B) describes where is sensor A relative to sensor B.
  • For example, depth_to_color, in D435i:
    • If we look from behind of the D435i, extrinsic from depth to color, means, where is the depth in relative to the color.
    • If we just look at the X coordinates, in the optical coordiantes (again, from behind) and assume that COLOR(RGB) sensor is (0,0,0), we can say that DEPTH sensor is on the right of RGB by 0.0148m (1.48cm).

d435i
administrator@perclnx466 ~/ros2_humble $ ros2 topic echo /camera/camera/extrinsics/depth_to_color
rotation:
- 0.9999583959579468
- 0.008895332925021648
- -0.0020127370953559875
- -0.008895229548215866
- 0.9999604225158691
- 6.045500049367547e-05
- 0.0020131953060626984
- -4.254872692399658e-05
- 0.9999979734420776
translation:
- 0.01485931035131216
- 0.0010161789832636714
- 0.0005317096947692335
---
  • Extrinsic msg is made up of two parts:
    • float64[9] rotation (Column - major 3x3 rotation matrix)
    • float64[3] translation (Three-element translation vector, in meters)

:::

Warning

When exporting vertices to PLY format (a common 3D file format), the RealSense SDK, since version 2.19.0, converts the points to a left-handed coordinate system. This conversion was implemented to ensure compatibility with MeshLab, a popular 3D viewing and editing tool, where the default viewpoint is configured for a left-handed coordinate system.