Planning with Search
In the PDDL section we saw that a sequence of actions that the agent needs to execute to reach the goal can be obtained using domain-independent planners. This section provides the background that connects such planner to search. To do so, it is instructive to look to problems that are simpler in terms of state and action representation. We zoom out from the factored representation that PDDL assumes and treat the state of the environment as atomic i.e. not decomposable.
Atomic state representations of an environment are adequate for a a variety of global planning tasks such as path planning. There, the scene or environment takes the form of a global map and the goal is to move the embodied agent from a starting state to a goal state. If we assume that the global map takes the form of a grid with a suitable resolution, each grid tile (or cell) represents a different atomic state than any other cell. Similar considerations can be made for other forms of the map e.g. a graph form.
Given such state representation, we will use search to find the action sequence that the agent must produce to reach a goal state. In addition we will be dealing with informed rather than blind search, where we are also given task-specific knowledge (that we use to develop suitable heuristics) to find the solution as we will see shortly.
Maps
We will develop the algorithm for the task at hand which is to find the path between a starting state and the goal state in a map. Not just any path but the minimum cost path when the state transition graph is revealed incrementally through a series of actions and associated individual costs (cost function). The task is depicted below.

A map of a parking lot as determined via postprocessing LIDAR returns. Obstacles colored in yellow are tall obstacles, brown obstacles are curbs, and green obstacles are tree branches that are of no relevance to ground navigation.
In practice, maps likes the one above are local both in terms of space (each snapshot is relative to the location of the agent) as well as in terms of time (at the time the agent took these measurements). We can take any map like the one above and form its discrete equivalent such as shown below. We usually call this type metric map and for the purposes of this chapter this is our search area and in it lie all possible feasible solutions, each is a sequence of actions distinguished by path cost. In this example, the least cost path is actually the geographically longer path - the line thickness for each of the two possible solutions in this figure is proportional to its cost.
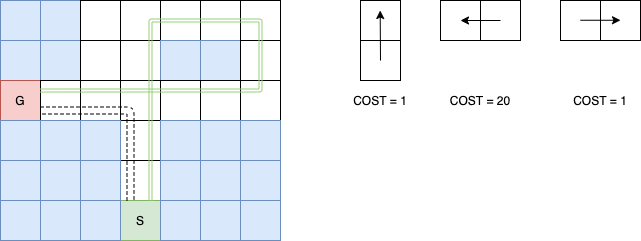
An example search area with action-cost function where left turns are penalized compared to right.This is common penalization in path planning for delivery vehicles.
The alternative map representation is topological where the environment is represented as a graph where nodes indicated significant grounded features and edges denote topological relationships (position, orientation, proximity etc.). Irrespectively of metric or topological representations, the forward search methods we focus on all function on graphs.