Maximum Likelihood (ML) Estimation of conditional models

The discussion in the marginal distribution is equivalently applicable to the conditional distribution \(p_{model}(\mathbf y | \mathbf x, \mathbf w)\) which governs supervised learning, \(y\) being the symbol of the label / target variable. Therefore all machine learning software frameworks offer excellent APIs on CE calculation.

\[ L(\mathbf w) = - \mathbb{E_{\mathbf x, \mathbf y \sim \hat p_{data}}} \log p_{model}(\mathbf y | \mathbf x; \mathbf w)\]

The attractiveness of the ML solution is that the CE (also known as log-loss) is general and we don’t need to re-design it when we change the model.

Visualizing the regression function - the conditional mean

It is now instructive to go over an example to understand that even the plain-old mean squared error (MSE), the objective that is common in the regression setting, falls under the same umbrella - its the cross entropy between \(\hat p_{data}\) and a Gaussian model.

Please follow the discussion associated with Section 5.5.1 of the Ian Goodfellow’s book or section 20.2.4 of Russell & Norvig’s book and these notes and consider the following figure for assistance to visualize the relationship of \(p_{data}\) and \(p_{model}\).

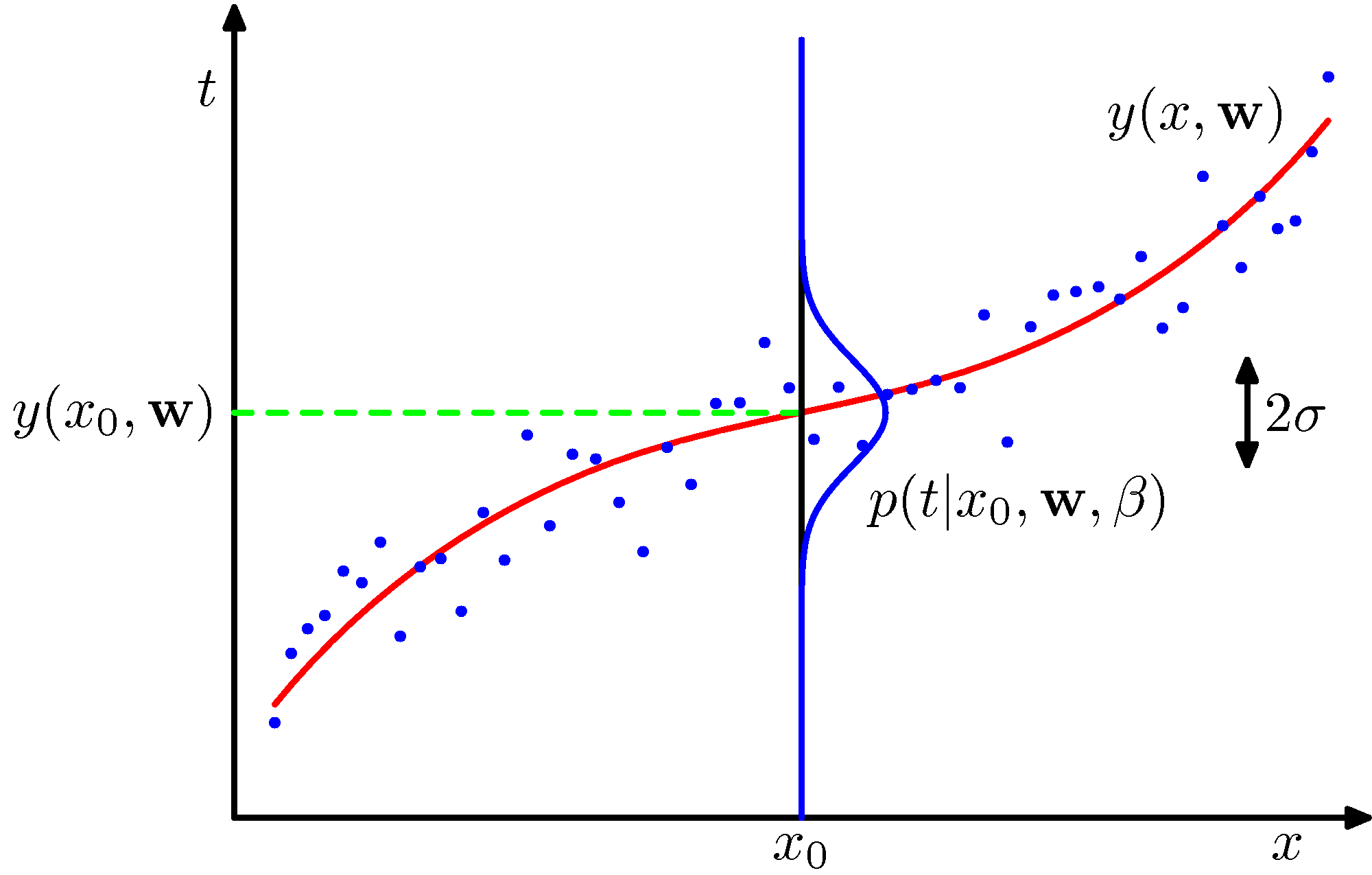Please replace the y-axis target variable \(t\) with \(y\). The green dashed line shows the mean of the \(p_{model}\) distribution.