Empirical Risk Minimization
Lets reflect on the MSE and how model complexity gives raise to various generalization errors.
\[MSE = \mathbb{E}[(\hat{y}_i - y_i)^2] = \mathrm{Bias}(\hat{y}_i)^2 + \mathrm{Var}(\hat{y}_i)\]
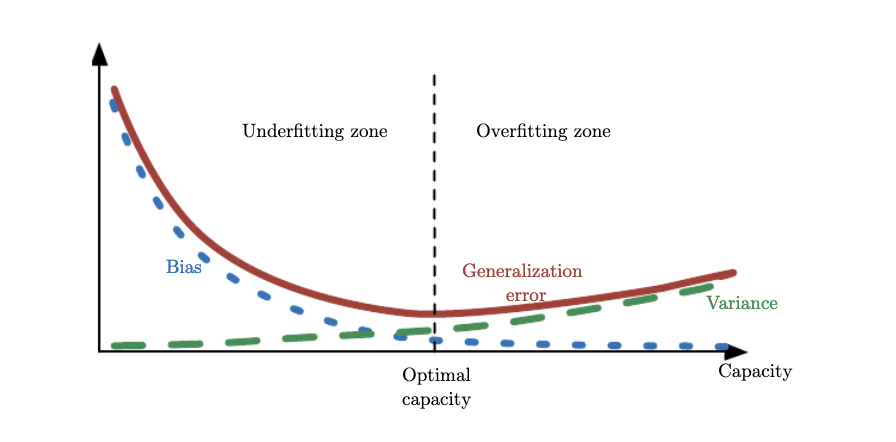
which means that the MSE captures both bias and variance of the estimated target variables and as shown in the plots above, increasing model capacity can really increase the variance of \(\hat{y}\). We have seen that as the \(\mathbf{w}\) is trying to exactly fit, or memorize, the data, it minimizes the bias (in fact for model complexity M=9 the bias is 0) but it also exhibits significant variability that is itself translated to \(\hat{y}\). Although the definition of model capacity is far more rigorous, we will broadly associate complexity with capacity and borrow the figure below from Ian Goodfellow’s book to demosntrate the tradeoff between bias and variance. What we have done with regularization is to find the \(\lambda\) that minimized generalization error aka. find the optimal model capacity.
Bias and Variance Decomposition during the training process
Apart from the composition of the generalization error for various model capacities, it is interesting to make some general comments regarding the decomposition of the generalization error (also known as empirical risk) during training. Early in training the bias is large because the predictor output is far from the target function. The variance is very small because the data has had little influence yet. Late in training the bias is small because the predictor has learned the underlying function. However if train for too long then the predictor will also have learned the noise specific to the dataset (overfitting). In such case the variance will be large because the noise varies between training and test datasets.
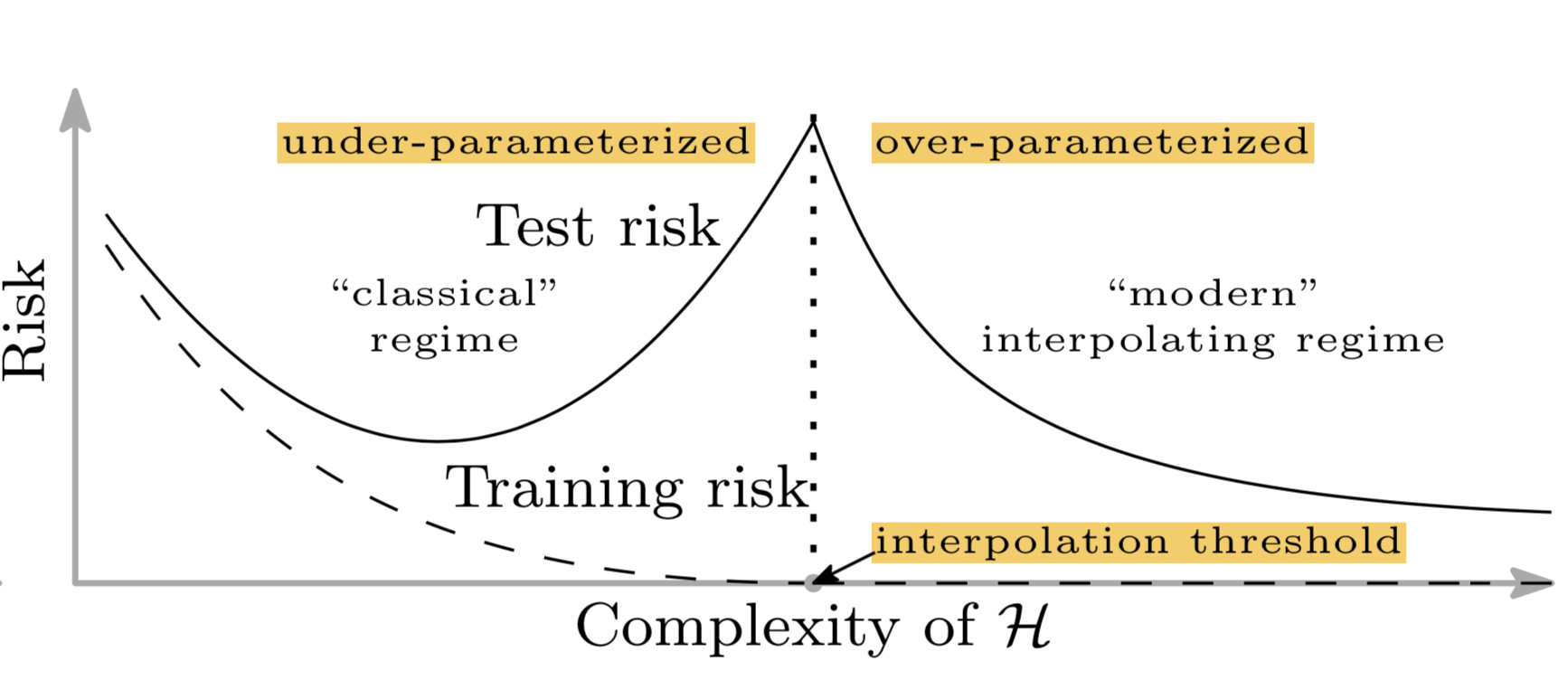
Notably for deep learning models, the risk curve is exhibiting a pleasant property that indicates that despite the increase in capacity, the generalization error is increasing initially and then enters a regime where the error decreases avoiding overfitting as shown in Figure 2.