Layer Normalization (LN)

Figure 1: Difference between Batch Normalization and Layer Normalization. LN operates across the feature dimensions for each sample independently, normalizing the activations in a trainable way - effectively its like the transpose of BN.

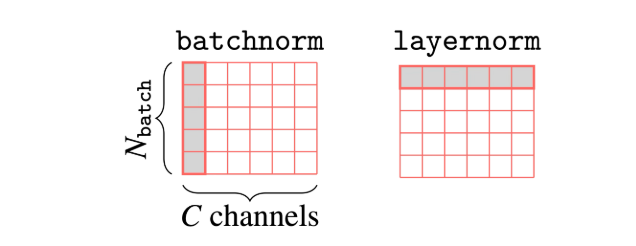
We saw that Batch Normalization (BN) is a technique that positions the activations in a trainable way and helps on training efficiency. However, it has some limitations, especially when dealing with small batch sizes. Since it operates across the batch dimension, it normalizes the activations for each feature/channel across the batch. This means that smaller batch sizes can result in inaccurate statistics. This is particularly true in LLMs that are often trained with large models that require small mini-batches due to memory constraints.

Therefore in certain architectures such as recurrent networks and transformers, we apply Layer Normalization. The layer normalization of an input vector \(x \in \mathbb{R}^d\) is computed as:

\[ \text{LayerNorm}(x) = \gamma \odot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta \]

where the mean \(\mu\) and variance \(\sigma^2\) are:

\[ \mu = \frac{1}{d} \sum_{i=1}^{d} x_i, \quad \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 \]

Here: - \(\gamma\) and \(\beta\) are learnable parameters (of shape \(d\)), - \(\epsilon\) is a small constant for numerical stability, - \(\odot\) denotes element-wise multiplication.

As shown in the figure, it operates across the feature dimensions for each sample independently, normalizing the activations in a trainable way - effectively its like the transpose of BN.