Motion Planning
Odometry Motion Model
Odometry is commonly obtained by integrating wheel encoders information; most commercial robots make such integrated pose estimation available in periodic time intervals (e.g., every tenth of a second).
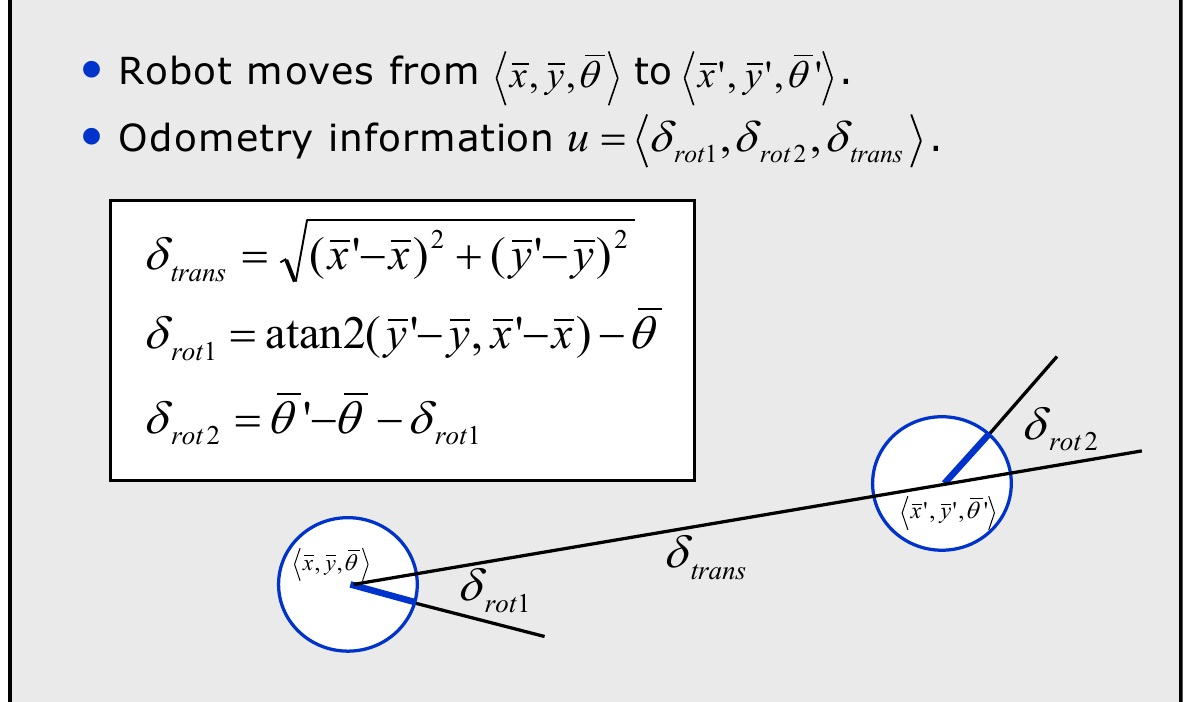


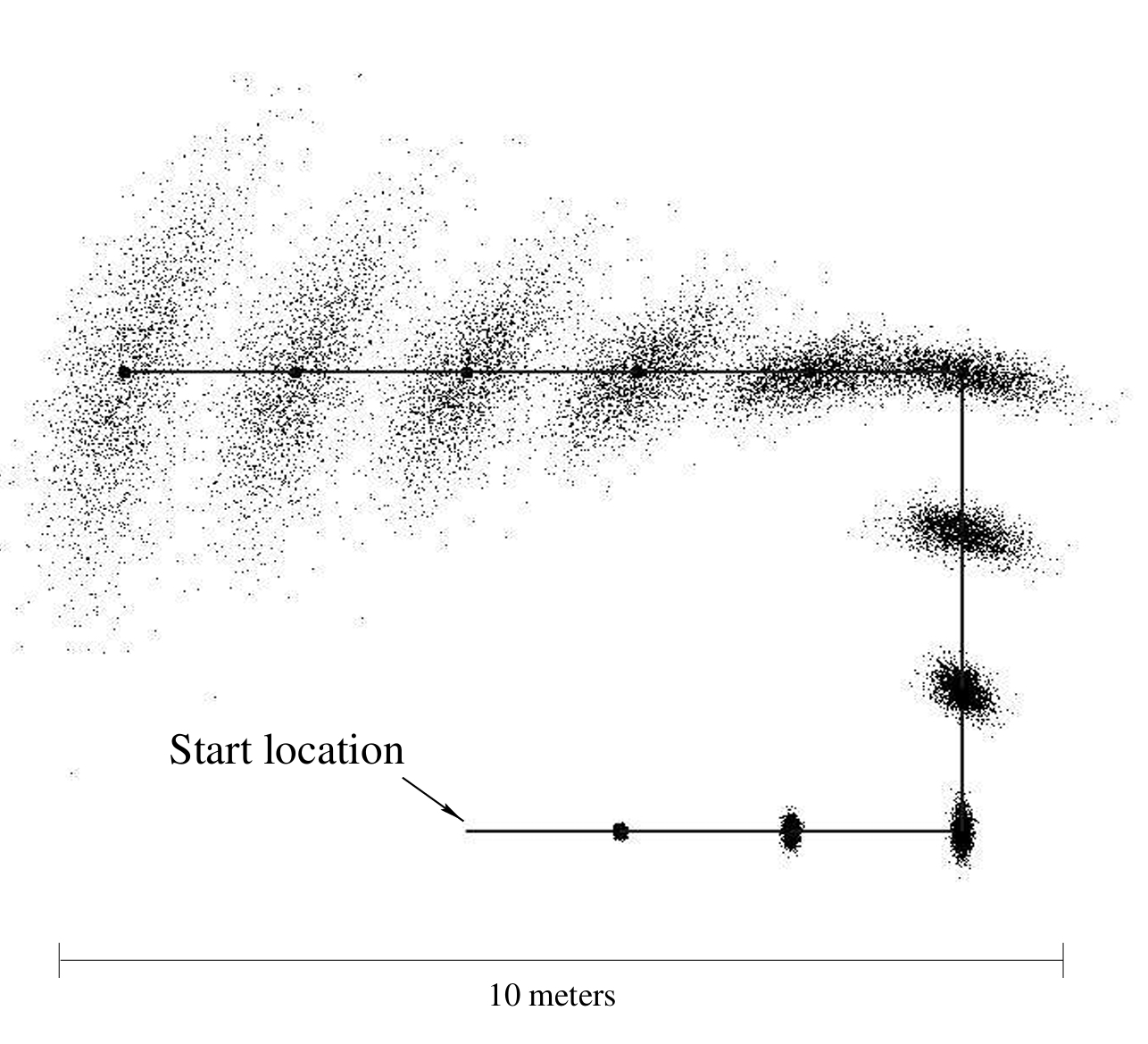
Wheel displacements derived from encoder readings produce noisy pose update: \[p(x_t \mid x_{t-1}, u_t) = p(\Delta \hat{rot}_1) p(\Delta \hat{trans}) p(\Delta \hat{rot}_2),\]
factorized by initial rotation, translation, final rotation.
Compute noisy components: \[\begin{aligned} \Delta rot_1 &= \operatorname{atan2}(y_t - y_{t-1}, x_t - x_{t-1}) - \theta_{t-1},\\ \Delta trans &= \sqrt{(x_t - x_{t-1})^2 + (y_t - y_{t-1})^2},\\ \Delta rot_2 &= \theta_t - \theta_{t-1} - \Delta rot_1. \end{aligned}\]
Sample corrupted increments:
\[\tilde{\Delta rot}_1 = \Delta rot_1 - \mathcal{N}(0, \alpha_1 \Delta rot_1^2 + \alpha_2 \Delta trans^2)\] and similarly for \(\tilde{\Delta trans}\), \(\tilde{\Delta rot}_2\).
Updated pose:
\[\begin{aligned} x_t &= x_{t-1} + \tilde{\Delta trans} \cos(\theta_{t-1} + \tilde{\Delta rot}_1),\\ y_t &= y_{t-1} + \tilde{\Delta trans} \sin(\theta_{t-1} + \tilde{\Delta rot}_1),\\ \theta_t &= \theta_{t-1} + \tilde{\Delta rot}_1 + \tilde{\Delta rot}_2. \end{aligned}\]
Velocity Motion Model
Given commanded \((v,\omega)\) and noise parameters \(\alpha_i\):
\[\begin{aligned} \hat v &= v + \mathcal{N}(0, \alpha_1 v^2 + \alpha_2 \omega^2),\\ \hat \omega &= \omega + \mathcal{N}(0, \alpha_3 v^2 + \alpha_4 \omega^2),\\ \hat \gamma &= \mathcal{N}(0, \alpha_5 v^2 + \alpha_6 \omega^2), \end{aligned}\]
then sample the next pose \((x_t,y_t,\theta_t)\) via standard velocity model equations.
\[\begin{aligned} x_t &= x_{t-1} - \frac{\hat v}{\hat \omega}\sin \theta_{t-1} + \frac{\hat v}{\hat \omega}\sin(\theta_{t-1}+\hat \omega \Delta t),\\ y_t &= y_{t-1} + \frac{\hat v}{\hat \omega}\cos \theta_{t-1} - \frac{\hat v}{\hat \omega}\cos(\theta_{t-1}+\hat \omega \Delta t),\\ \theta_t &= \theta_{t-1} + \hat \omega \Delta t + \hat \gamma \Delta t. \end{aligned}\]
If \(|\hat \omega| < \epsilon\) treat as straight motion:
\[x_t = x_{t-1} + \hat v \Delta t \cos \theta_{t-1}, \quad y_t = y_{t-1} + \hat v \Delta t \sin \theta_{t-1}, \quad \theta_t = \theta_{t-1} + \hat \gamma \Delta t.\]