Probability Assignment#
To get full credit in this assignment you need to use only numpy or numba libraries and include adequate explanation of the code in either markdown cells or code comments. Sometimes you need to type equations - type equations in latex math notation.
Question 1 (20 points)#
Generate N uniform distributed over the interval [0,1] random variables \(\{x_1, \dots x_N\}\).
Compute their mean and after repeating such computation \(m\) times, plot the histogram as \(N\) takes values \({1, 5, 10, 20}\).
Provide a justification of the resultant histogram by reading about the Cenral Limit Theorem.
# Type the Python code here
Question 2 (20 points)#
The exercise refers to Example 6.6 of the Math for ML book.
Simulate and plot the bivariate normal distribution with the shown parameters.
You need to use the Cholesky factorization for the simulation.
Question 3 (30 points)#
Simulate coin tossing experiments involving a biased coin with probability of heads is \(p_H=0.6\) and \(n_{trials} = [0, 5, 15, 50, 500]\) (10 points)
Assume you don’t know \(p_H\) and you need to estimate it. Plot the estimate as a function of the number of trials. Comment on the accuracy of the estimate for small vs. large trials. (10 points)
Calculate the variance of the estimated \(p_H\) (10 points). Comment on its behavior as a function of the true \(p_H\) itself and the \(n_{trials}\).
# Type the Python code here
Question 4 (30 points)#
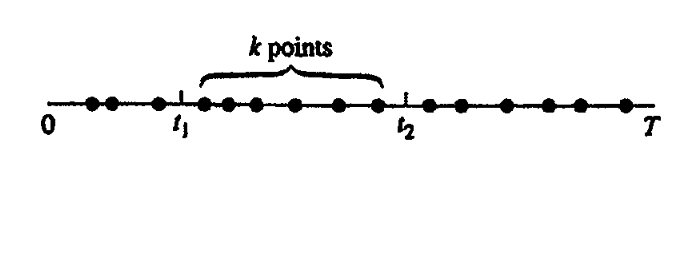
We monitor server faults in a data center over a period of T units of time and represents each occurring fault as a point on the line. What is the probability that k faults take place between \(t_1\) and \(t_2\) if \(n\) total points were recorded ? (10 points)
We collected a very large set of faults \(n \rightarrow \infty\) over a long measurement interval \(T \rightarrow \infty\) and we observed that on average faults occur with a rate of \(\lambda = \frac{n}{T}\). This allows us to model the probability of \(k_a\) points in an interval \(t_a\) as Poisson. Suppose that we measure \(k_a\) and \(k_b\) faults in two consecutive intervals of durations \(t_a=(t_1, t_2)\) and \(t_b=(t_2, t_3)\) respectively where \(t_a+t_b < T\), write the expression of the joint probability $\(p(k_a \in t_a, k_b \in t_b)\)$. (10 points)
Suppose now that we need to schedule personnel to replace these servers and we are interested to use the fault data to estimate the probability of $\(p(k_a \in t_a | k_c \in t_c)\)\( where \)t_c=t_a + t_b$. Write the expression of this conditional probability. (10 points)
Write your answer here and use Latex math notation for math. If you prefer write the math with pencil and scan the writeup in a png image that you can insert here using



