Gradient Boosting#
Like AdaBoost, Gradient Boosting works by sequentially adding predictors to an ensemble, each one correcting its predecessor. However, instead of tweaking the example weights at every iteration, this method tries to fit the new predictor to the residual errors made by the previous predictor.
Please go through the excellent explanation of Gradient boosting from explained.ai to understand the intuition behind it:
Gradient Boosting for Regression Example#
The complete understanding of gradient boosting (and boosting in general) requires mathematical treatment around function-space optimization as in Friedma’s original paper. Here we look at the solution from a practical perspective and attempt to understand it with the use of a regression example as shown below.
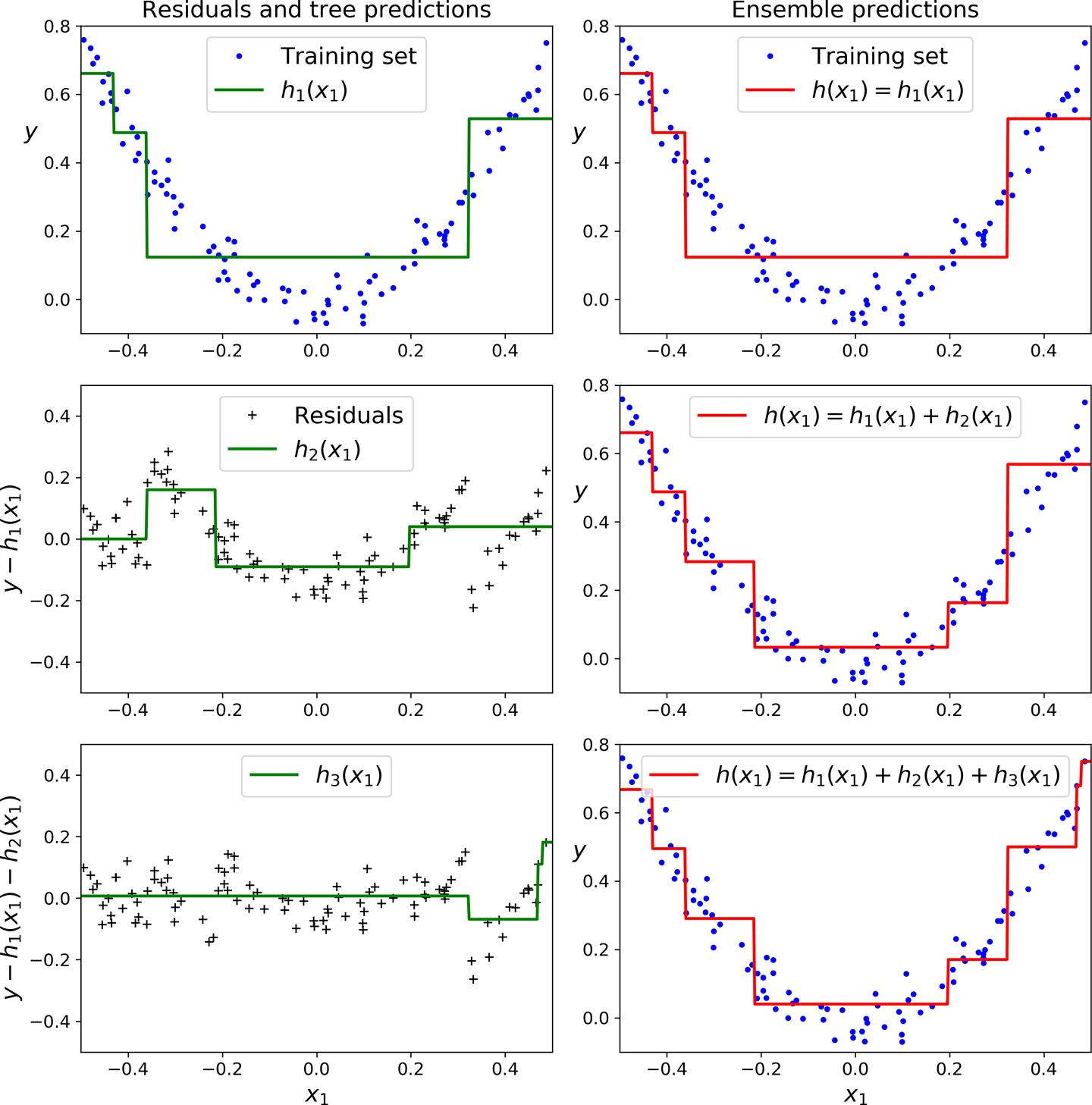In this depiction of Gradient Boosting, the first predictor (top left) is trained normally, then each consecutive predictor (middle left and lower left) is trained on the previous predictor’s residuals; the right column shows the resulting ensemble’s predictions which is equal to the sum of the predictions of the trees involved.
Predictions improve as the number of trees grows but we need to know when to stop.
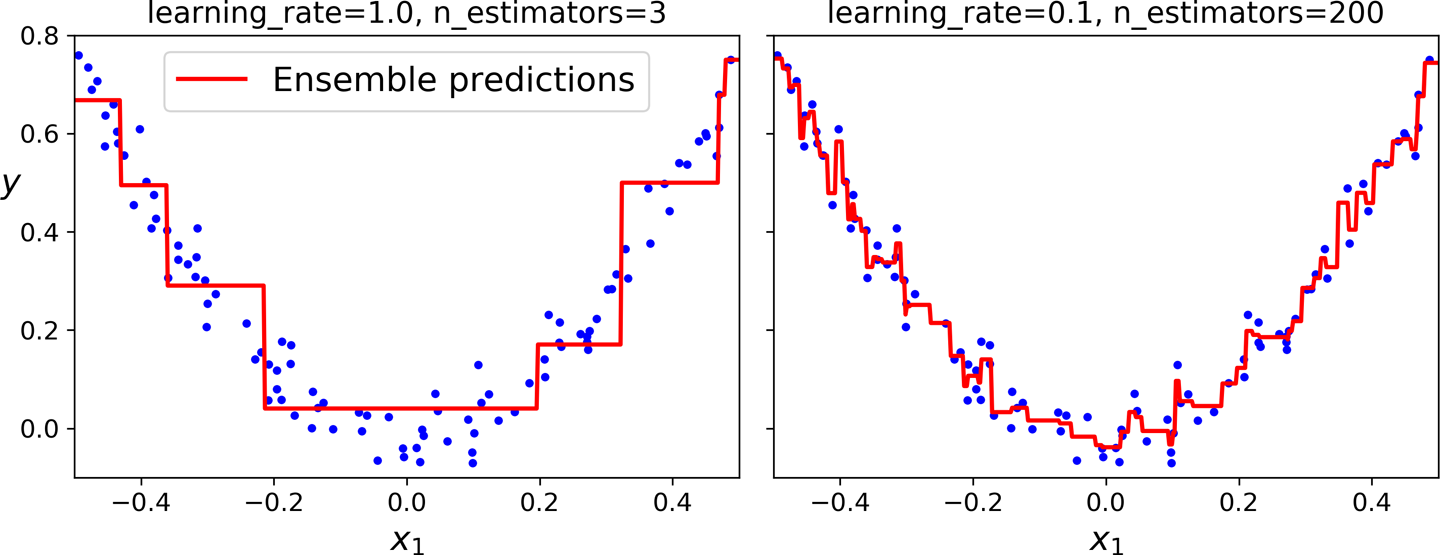On the left we dont have enough trees to fit the training set, while the one on the right we have too many trees and overfit the training set.
Gradient Boosting Libraries#
In practice, do not use sklearn for gradient boosting. XGBoost and LightGBM are standard tools for winning Kaggle competitions. Given that gradient boosting dominates performance wise many methods in classical machine learning with structured data (e.g. tabular data), XGBoost is also the standard library to try first in these type of problems. It offers also automatic ways of stopping at the right number of trees in the ensemble and other enhancements. This write up explains XGBoost internal design.
Gradient Boosting and Maximum Likelihood#
The MLE method that dominats all differential prediction machines today, jointly optimizes the parameters for across the whole population of hypotheses, such as in linear regression where the components are based on a selected set of basis functions. In Gradient boosting, we only optimize the parameters of the new hypothesis that is added to the ensemble i.e. we have a sequential optimization process.