import numpy as np
# Optional SciPy speed-up
try:
from scipy.spatial import cKDTree as _cKDTree # type: ignore[import-not-found]
_HAS_SCIPY = True
except Exception:
_cKDTree = None # type: ignore[assignment]
_HAS_SCIPY = False
def nearest_neighbors(query: np.ndarray, ref: np.ndarray):
"""
Return (distances, indices) of nearest neighbors in 'ref' for each row in 'query'.
Uses cKDTree if available; otherwise a vectorized NumPy fallback.
"""
if _HAS_SCIPY and _cKDTree is not None:
tree = _cKDTree(ref)
dists, idx = tree.query(query, k=1)
return dists, idx
QN = query.shape[0]
idx = np.empty(QN, dtype=int)
dists = np.empty(QN, dtype=float)
chunk = 4096
for start in range(0, QN, chunk):
end = min(QN, start + chunk)
diff = query[start:end, None, :] - ref[None, :, :]
dist2 = np.sum(diff * diff, axis=2)
nn = np.argmin(dist2, axis=1)
idx[start:end] = nn
dists[start:end] = np.sqrt(dist2[np.arange(end - start), nn])
return dists, idx
def best_rigid_transform(A: np.ndarray, B: np.ndarray):
"""
Given paired points A, B of shape (N, d), compute R, t with R in SO(d) minimizing ||R A + t - B||_F^2.
"""
assert A.shape == B.shape
cA = A.mean(axis=0)
cB = B.mean(axis=0)
AA = A - cA
BB = B - cB
H = AA.T @ BB
U, S, Vt = np.linalg.svd(H)
R = Vt.T @ U.T
if np.linalg.det(R) < 0:
Vt[-1, :] *= -1
R = Vt.T @ U.T
t = cB - R @ cA
return R, t
def icp_point_to_point(
P: np.ndarray, Q: np.ndarray, R0: np.ndarray = None, t0: np.ndarray = None, max_iters: int = 50, tol: float = 1e-6
):
"""
Point-to-point ICP that returns (R, t, history).
P: source (N, d), Q: target (M, d).
"""
d = P.shape[1]
R = np.eye(d) if R0 is None else R0.copy()
t = np.zeros(d) if t0 is None else t0.copy()
prev_err = np.inf
history = []
for it in range(max_iters):
P_tr = (R @ P.T).T + t
dists, idx = nearest_neighbors(P_tr, Q)
Q_match = Q[idx]
R_delta, t_delta = best_rigid_transform(P_tr, Q_match)
R = R_delta @ R
t = R_delta @ t + t_delta
mean_err = float(np.mean(dists))
history.append((it, mean_err))
if abs(prev_err - mean_err) < tol:
break
prev_err = mean_err
return R, t, historyIterative Closest Point (ICP)
- Besl & McKay (1992) for the original method.
- Hartley & Zisserman (Multiple View Geometry) for rigid alignment via SVD.
- Thrun, Burgard, Fox (Probabilistic Robotics) for SLAM context.
Problem formulation and SVD solution
Given matched pairs (p_i, q_i), the least squares problem \[ \min_{R\in SO(d),\,t\in\mathbb{R}^d} \sum_i \lVert R p_i + t - q_i\rVert^2 \] has the closed-form solution via centroid subtraction and SVD of \[ H=\sum_i (p_i-\bar p)(q_i-\bar q)^\top,\quad H=USV^\top,\quad R^\star=VU^\top,\quad t^\star=\bar q - R^\star \bar p. \] ICP alternates nearest-neighbor correspondence with this closed-form update.
Synthetic experiment in 3D
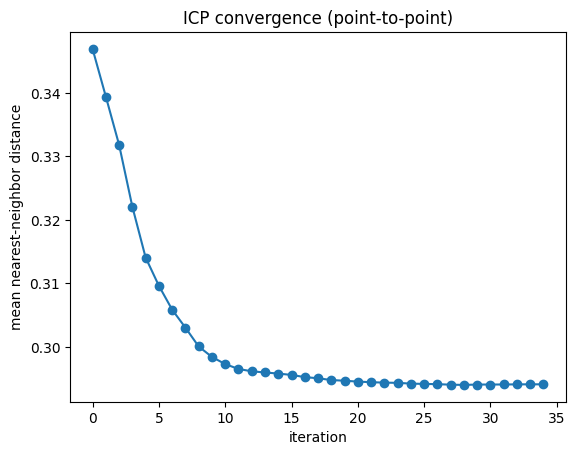
We generate a random target cloud Q, apply a known rigid transform and small noise to produce P, and run ICP to estimate the transform. We then compare with ground truth and plot the convergence of the mean nearest-neighbor distance.
# pip install matplotlib # when running locally, if missing
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(7)
Q = np.random.randn(500, 3)
def random_rotation_3d():
A = np.random.randn(3, 3)
Qr, _ = np.linalg.qr(A)
if np.linalg.det(Qr) < 0:
Qr[:, -1] *= -1
return Qr
R_true = random_rotation_3d()
t_true = np.array([0.8, -0.3, 0.5])
noise = 0.01 * np.random.randn(*Q.shape)
P = (R_true @ Q.T).T + t_true + noise
R_est, t_est, hist = icp_point_to_point(P, Q, max_iters=100, tol=1e-8)
# Ground-truth for the estimated mapping (P -> Q) is the inverse of how P was generated
R_gt = R_true.T
t_gt = -R_true.T @ t_true
def rot_angle_deg(R):
# geodesic distance on SO(3)
tr = np.clip((np.trace(R) - 1) / 2.0, -1.0, 1.0)
return np.degrees(np.arccos(tr))
R_err = R_est @ R_gt.T
t_err = t_est - t_gt
print("Ground truth (inverse) R_gt = R_true^T:\n", R_gt)
print("Estimated R_est:\n", R_est)
print("\nGround truth (inverse) t_gt = -R_true^T t_true:", t_gt)
print("Estimated t_est:", t_est)
print("\nRotation error (deg):", rot_angle_deg(R_err))
print("Translation error (L2):", np.linalg.norm(t_err))
# RMS alignment error using true correspondences (same indices)
P_aligned = (R_est @ P.T).T + t_est
rms_true_pairs = np.sqrt(np.mean(np.sum((P_aligned - Q) ** 2, axis=1)))
print("RMS alignment error to true pairs:", rms_true_pairs)
iters = [h[0] for h in hist]
errs = [h[1] for h in hist]
plt.figure()
plt.plot(iters, errs, marker="o")
plt.xlabel("iteration")
plt.ylabel("mean nearest-neighbor distance")
plt.title("ICP convergence (point-to-point)")
plt.show()Ground truth (inverse) R_gt = R_true^T:
[[-0.30130898 -0.10656241 0.94755335]
[ 0.75309952 -0.63611162 0.16793784]
[ 0.58485384 0.76420315 0.27191824]]
Estimated R_est:
[[ 0.9895734 0.07507073 -0.12291813]
[-0.08181471 0.99535393 -0.05076323]
[ 0.11853621 0.06029046 0.99111767]]
Ground truth (inverse) t_gt = -R_true^T t_true: [-0.26469822 -0.87728202 -0.37458125]
Estimated t_est: [-0.34373394 0.1651141 -0.42091583]
Rotation error (deg): 150.5185966108678
Translation error (L2): 1.0464144519643552
RMS alignment error to true pairs: 2.6873782799382413