Vectors
Vectors
Most of the material in this section was borrowed from this excellent series of Essence of Linear Algebra youtube videos
The Physics, Computer Science and Math perspective on vectors
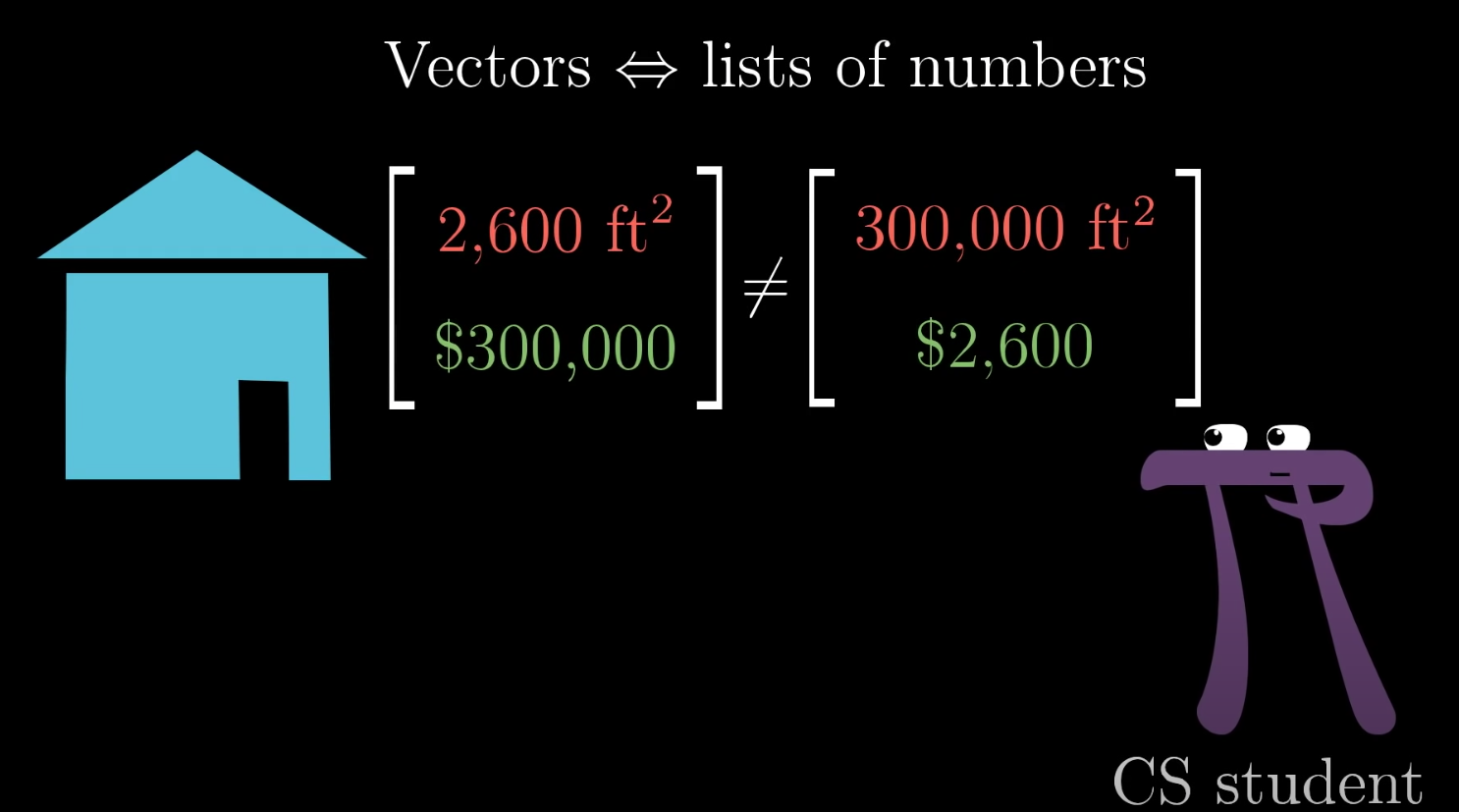
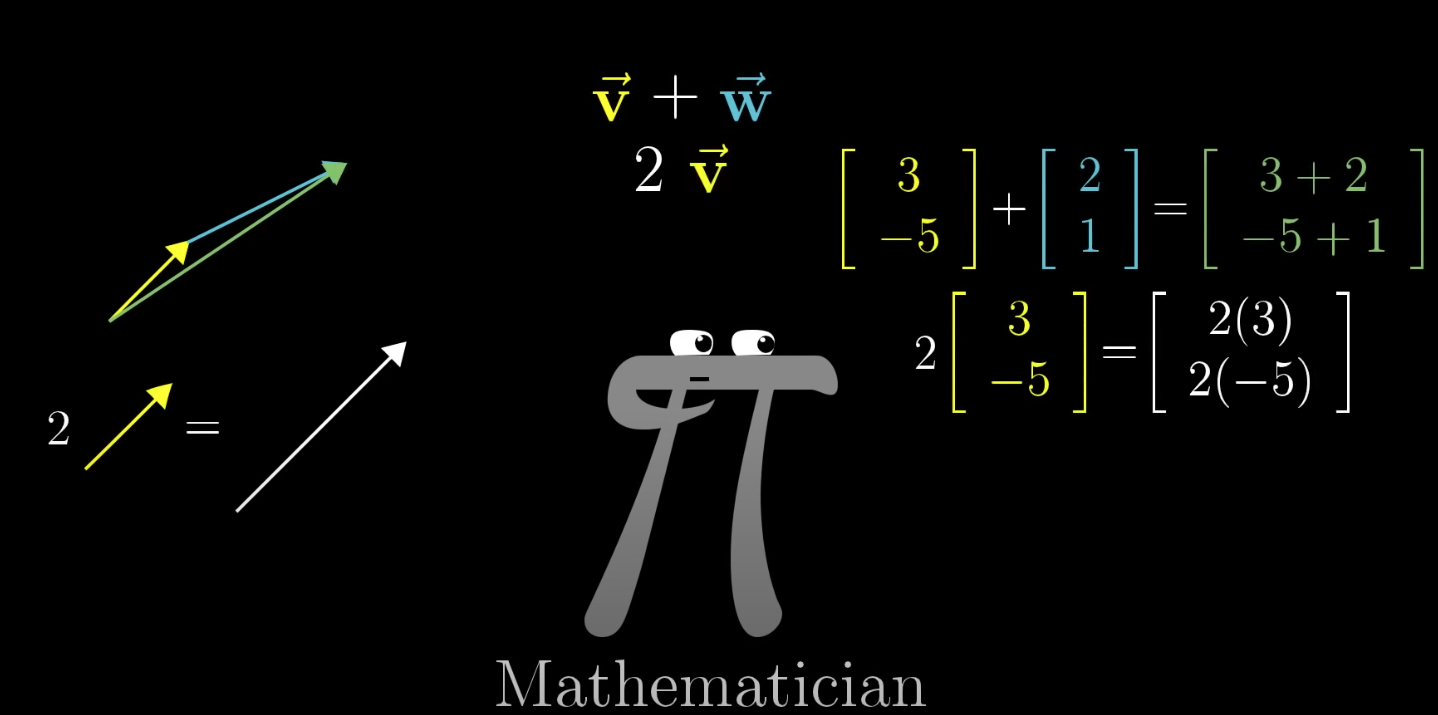
Coordinate systems and vector operations
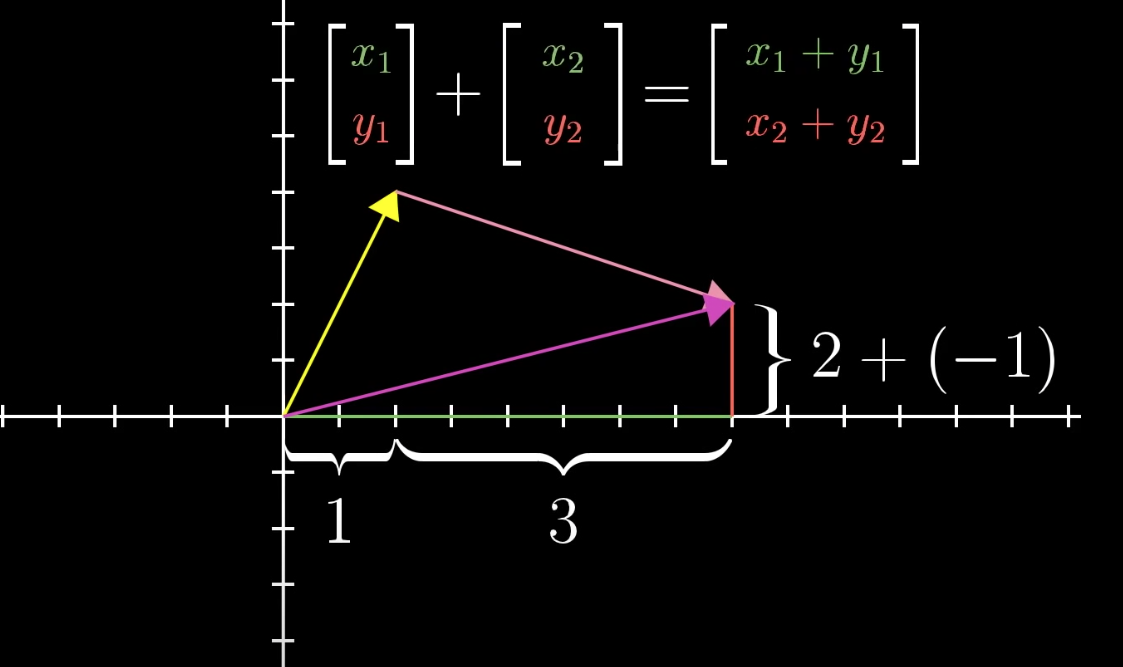 Notice the typo - its \([x_1+x_2, y_1+y_2]\)
Notice the typo - its \([x_1+x_2, y_1+y_2]\)
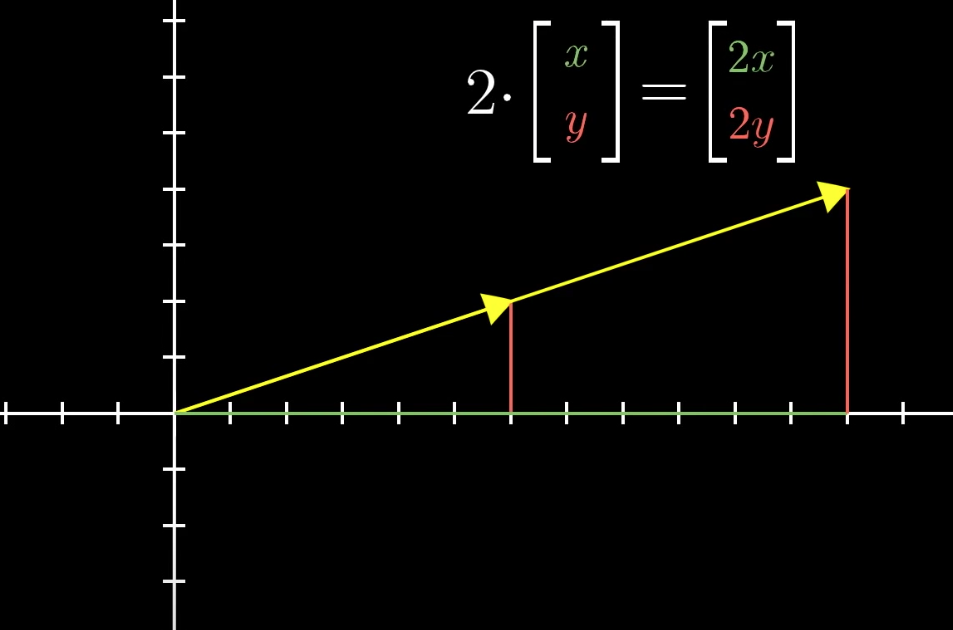
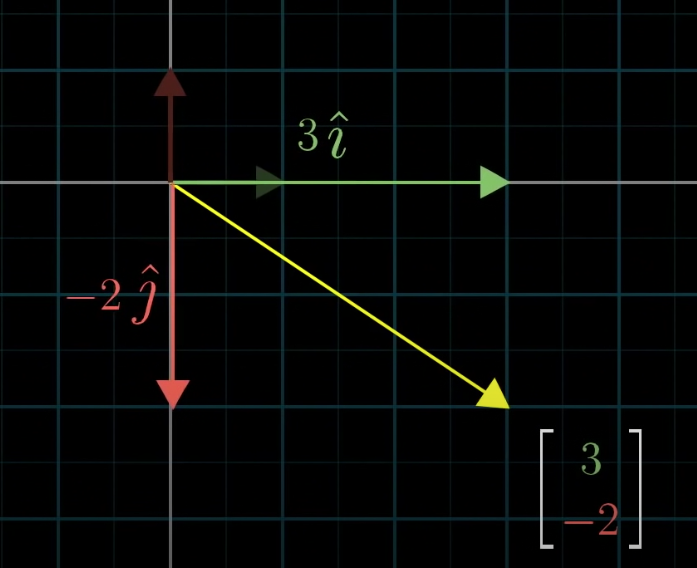 \(i\) and \(j\) are the basis vectors of the xy coordinate system. But these are not the only basis vectors that we can have.
\(i\) and \(j\) are the basis vectors of the xy coordinate system. But these are not the only basis vectors that we can have.
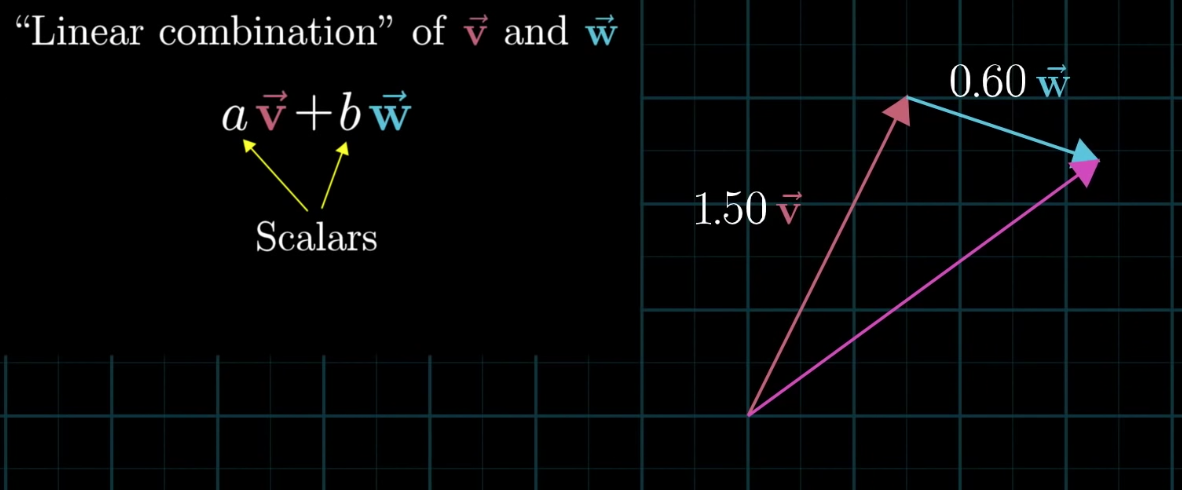 Every 2D vector can be expressed as a linear combination of two vectors
Every 2D vector can be expressed as a linear combination of two vectors
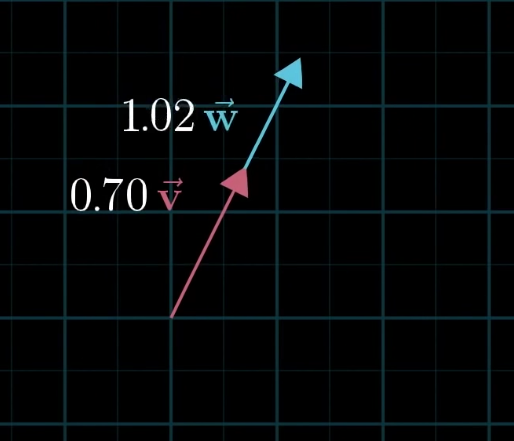 Not all vectors are good choices for creating a span. For example, these two vectors cant span the 2D space - they can only span a single line. \(v\) and \(w\) are then called linearly dependent.
Not all vectors are good choices for creating a span. For example, these two vectors cant span the 2D space - they can only span a single line. \(v\) and \(w\) are then called linearly dependent.
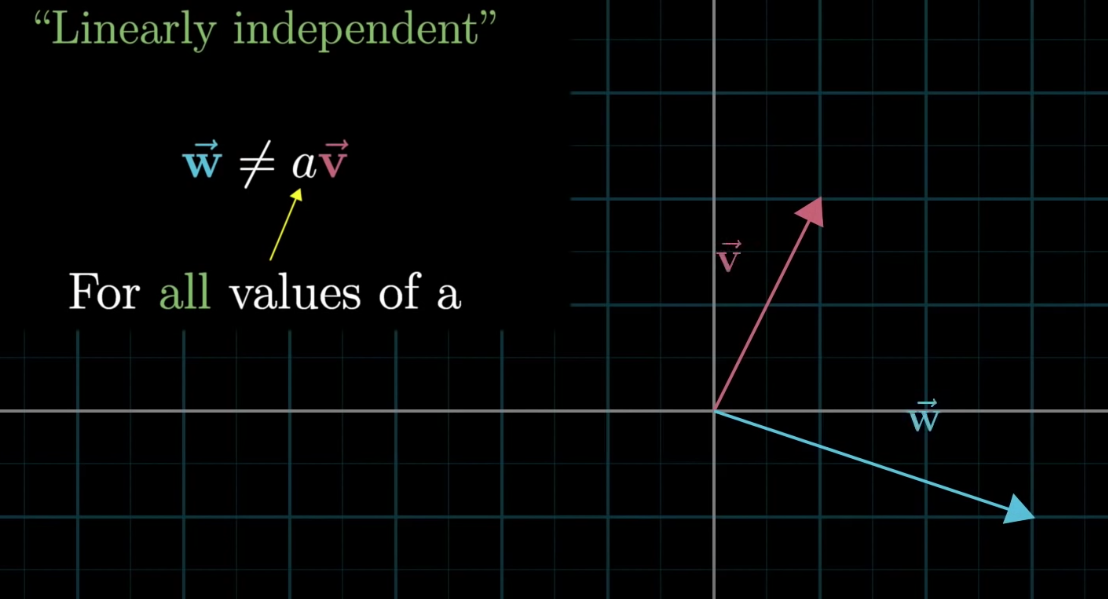 These two vectors span the full 2D space - \(v\) and \(w\) are then called linearly independent.
These two vectors span the full 2D space - \(v\) and \(w\) are then called linearly independent.
 Such set of vectors that are linearly independent and span the full space are called the basis vectors of a vector space
Such set of vectors that are linearly independent and span the full space are called the basis vectors of a vector space