import numpy as np
def stochastic_robot_cleaning_v1():
# Initialization
state = [0, 1, 2, 3, 4, 5] # Set of states
action = [-1, 1] # Set of actions
# Make all (state, action) pairs
A, B = np.meshgrid(state, action)
C = np.column_stack((A.flatten(), B.flatten()))
D1 = C # D includes all possible combinations of (state, action) pairs
# Make all (state, action) pairs indices
A, B = np.meshgrid(np.arange(len(state)), np.arange(len(action)))
C = np.column_stack((A.flatten(), B.flatten()))
D2 = C # D includes all possible combinations of (state, action) pairs indices
D = np.column_stack((D1, D2))
Q = np.zeros((len(state), len(action))) # Initial Q can be chosen arbitrarily
Qold = Q # Save a backup to compare later
L = 15 # Maximum number of iterations
gamma = 0.5 # Discounting factor
epsilon = 0.001 # Final error to stop the algorithm
# Deterministic Q-iteration algorithm
for l in range(1, L + 1):
print(f'iteration: {l}')
for ii in range(D.shape[0]):
XP, P, R = model(D[ii, 0], D[ii, 1]) # Includes the next states and the probability
I1 = np.where(D[:, 0] == XP[0])[0] # Find the next state in the pair-matrix D
I2 = np.where(D[:, 0] == XP[1])[0]
I3 = np.where(D[:, 0] == XP[2])[0]
Q[D[ii, 2], D[ii, 3]] = P[0] * (R[0] + gamma * np.max(Q[I1, :])) + \
P[1] * (R[1] + gamma * np.max(Q[I2, :])) + \
P[2] * (R[2] + gamma * np.max(Q[I3, :]))
if np.abs(np.sum(Q - Qold)) < epsilon:
print('Epsilon criteria satisfied!')
break
else:
Qold = Q
# Show the results
print('Q matrix (optimal):')
print(Q)
C = np.argmax(Q, axis=1) # Finding the max values
print('Q(optimal):')
print(C)
print('Optimal Policy:')
print('*')
print([action[C[1]], action[C[2]], action[C[3]], action[C[4]]])
print('*')
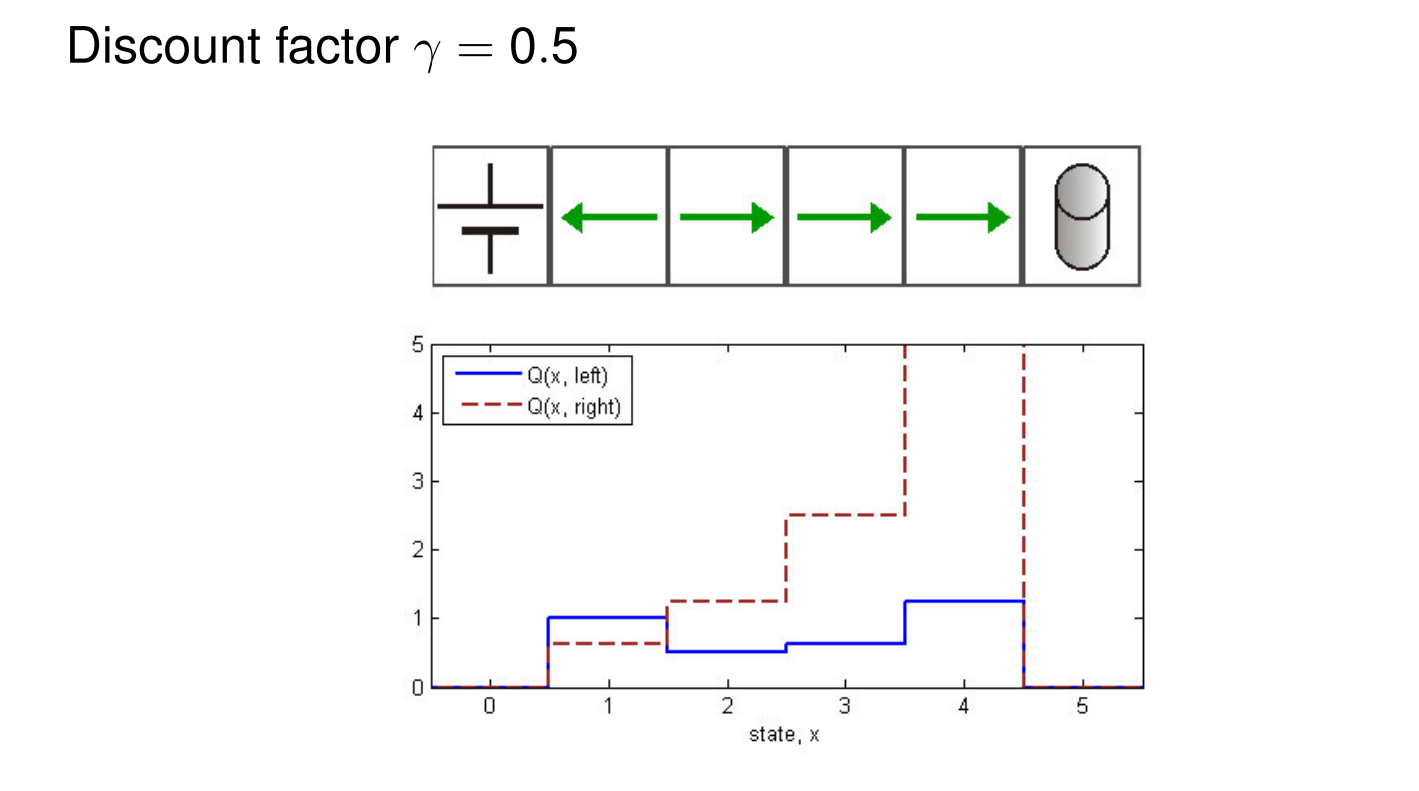
Cleaning Robot - Stochastic MDP
The following code shows the estimation of the q value function for a policy, the optimal q_star and the optimal policy for the cleaning robot problem in the strochastic case.
# Find the possible next states together with their probability value
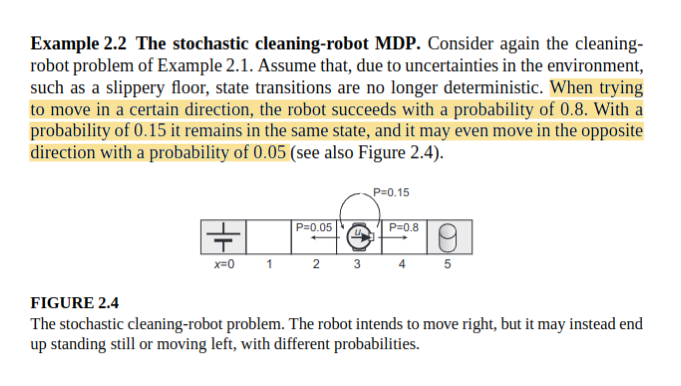
def model(x, u):
if x == 0 or x == 5:
xp = [x, x, x]
else:
xp = [x - u, x, x + u]
p = [prob(x, u, xp[0]), prob(x, u, xp[1]), prob(x, u, xp[2])]
r = [reward(x, u, xp[0]), reward(x, u, xp[1]), reward(x, u, xp[2])]
return xp, p, r
# This function is the transition model of the robot
# The inputs are: the current state, the chosen action, and the next desired state
# The output is the probability for going to the next state considering the stochasticity
# In the deterministic case, the model gives the next state, but in the stochastic case,
# the model gives the probability for going to the next state.
def prob(x, u, xp):
if x == 0 or x == 5:
if xp == x:
return 1
else:
return 0
elif 1 <= x <= 4:
if xp == x:
return 0.15
elif xp == x + u:
return 0.8
elif xp == x - u:
return 0.05
else:
return 0
else:
return 0
# This function is the reward function for the task (stochastic)
# The inputs are: the current state, the chosen action, and the next state
# The output is the expected reward in the next state
# The reward actually doesn't depend on the chosen action, in this case
def reward(x, u, xp):
if x != 5 and xp == 5:
return 5
elif x != 0 and xp == 0:
return 1
else:
return 0
# Call the main function
stochastic_robot_cleaning_v1()