Online Bayesian Regression
Lets us consider an instructive example of applying the Bayesian approach in an online learning setting (streaming data arriving over the wire). In this example where the underlying target function is \(p_{data}(x, \mathbf w) = w_0 + w_1 x + n\) This is the equation of a line. In this example its parametrized with \(a_0=-0.3, a_1=0.5\) and \(n \in \mathcal N(0, \sigma=0.2)\). To match the simple inference exercise that we just saw, we draw the equivalent PGM
Bayesian Linear Regression example - please replace \(t\) with \(y\) to match earlier notation in these notes
The Bayesian update of the posterior can be intuitively understood using a graphical example of our model of the form:
\[g(x,\mathbf{w})= w_0 + w_1 x\]
The reason why we pick this example is illustrative as the model has just two parameters and is amendable to visualization. The update needs a prior distribution over \(\mathbf w\) and a likelihood function. As prior we assume a spherical Gaussian
\[p(\mathbf w | \alpha) = \mathcal N(\mathbf w | \mathbf 0, \alpha^{-1} \mathbf I)\]
with \(\alpha = 0.2\). We starts in row 1 with this prior and at this point there are no data and the likelihood is undefined while every possible linear (line) hypothesis is feasible as represented by the red lines. In row 2, a data point arrives and the the Bayesian update takes place: the previous row posterior becomes the prior and is multiplied by the current likelihood function. The likelihood function and the form of the math behind the update are as shown in Bishop’s book in section 3.3. Here we focus on a pictorial view of what is the update is all about and how the estimate of the posterior distribution \(p(\mathbf w | \mathbf y)\) ultimately (as the iterations increase) it will be ideally centered to the ground truth (\(\mathbf a\)).
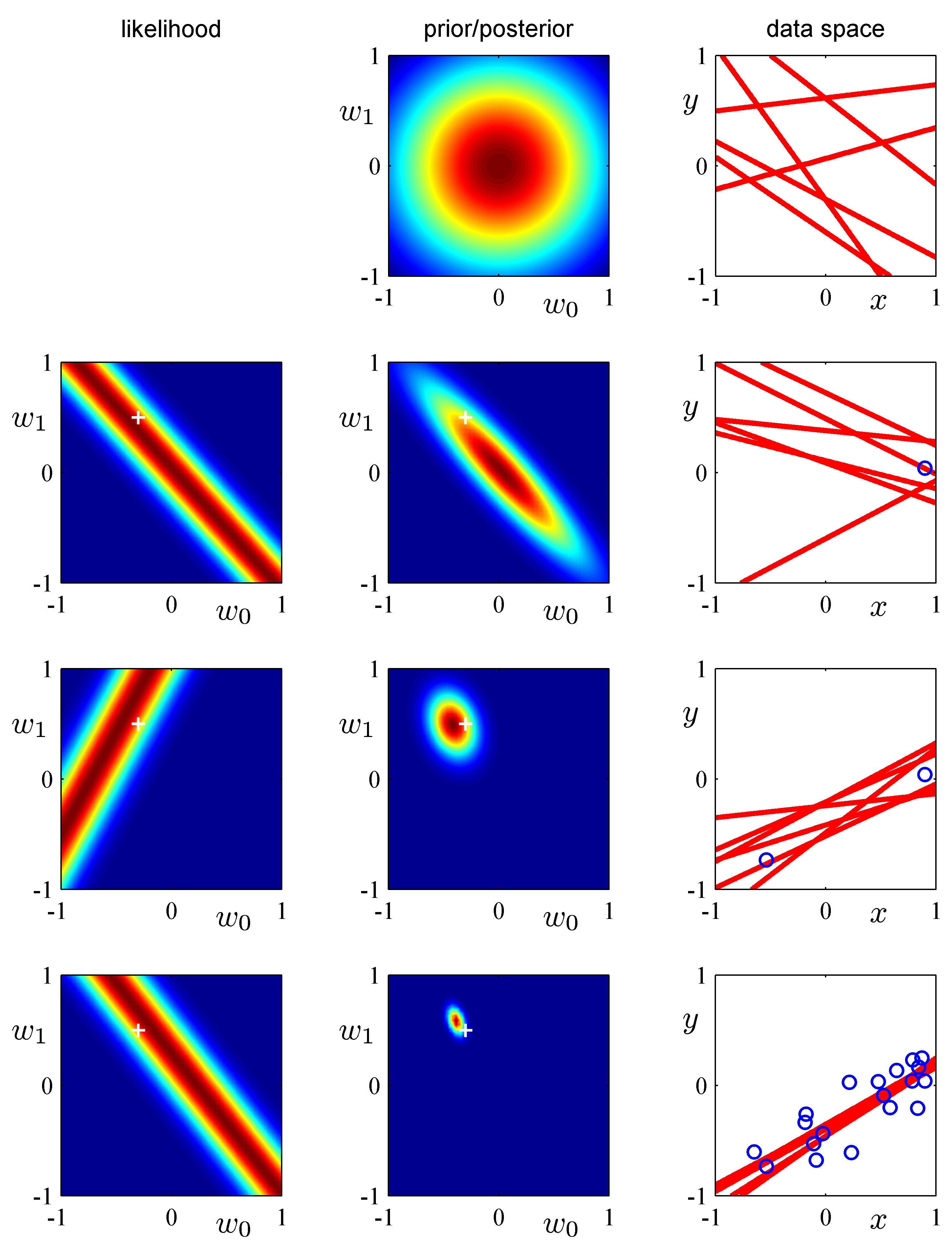 Instructive example of Bayesian learning as data points are streamed into the learner. Notice the dramatic improvement in the posterior the moment the 2nd data point arrives. Why is that?
Instructive example of Bayesian learning as data points are streamed into the learner. Notice the dramatic improvement in the posterior the moment the 2nd data point arrives. Why is that?
Bayesian Regression implementation
Notice in the notebook the two of the three broad benefits of the Bayesian approach:
- Compatibility with online learning - online learning does not mean necessarily that the data arrive over the ‘wire’ but it means that we can consider few data at a time.
- Adjustment of the predictive uncertainty (cov) to the sparsity of the data.
- Incorporation of external beliefs / opinions that can be naturally expressed probabilistically.