Probability Theory - Assignment A
Probability Theory - Assignment A
Exercise 1 (2 x 12.5 points)
A data scientist develops a model of the mortality probability distribution function
\[p(t) = 3 \times 10^{-9} t^2(100-t)^2, 0 \le t \le 100 ~\text{years}\]
\(p(t)\) is 0.0 outside the above range of \(t\).
What is the probability that a person will die between 60 and 70.
What is the probability that a person will die between 60 and 70, given that was alive at 60.
Exercise 2 (2 x 12.5 points)
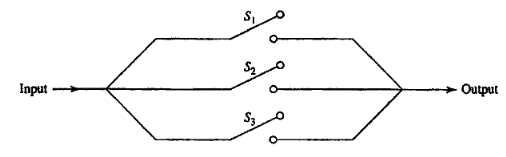
Three switches connected in parallel operate independently. Each switch remains closed with probability \(p\).
Find the probability of receiving an input signal at the output.
Find the probability that switch \(S_i\) is open given that an input signal is received at the output.
Exercise 3 (2 x 12.5 points)
Make yourself familiar with the multinomial distribution
Each trial involves throwing a die with 10 faces/sides. All faces are equally probable aka the die is not biased. Calculate the probability of the counts of outcome “2” if we performed \(n=1000\) trials.
Simulate n independent trials of the multinoulli (categorical distribution) compliant to the specification of (a). Plot the probability in (a) as a function of n independent trials (n=10-1000). Write your conclusions with respect to the behavior of the estimated probability as \(n\) increases.
NOTE: Submit this exercise in a colab notebook with permissions set to the professor and grader to be able to view.
Exercise 4 (25 points)
Replicate the Figure 1 plots of this writeup.
NOTE: Submit this exercise in a colab notebook with permissions set to the professor and grader to be able to view.