Neural Network Assignment
Neural Networks Assignment
Problem Set 1 (60 points. 10 points per question)
The TensorFlow Playground is a handy neural network simulator built by the TensorFlow team. In this exercise, you will train several binary classifiers in just a few clicks, and tweak the model’s architecture and its hyperparameters to gain some intuition on how neural networks work and what their hyperparameters do.
Try training the default neural network by clicking the Run button (top left). Notice how it quickly finds a good solution for the classification task. The neurons in the first hidden layer have learned simple patterns, while the neurons in the second hidden layer have learned to combine the simple patterns of the first hidden layer into more complex patterns. Why that is?
Activation functions. Try replacing the tanh activation function with a ReLU activation function, and train the network again. Does it find the solution faster or slower? Why is that?
The risk of local minima. Modify the network architecture to have just one hidden layer with three neurons. Train it multiple times (to reset the network weights, click the Reset button next to the Play button). Why the training time has a wide variability?
Remove one neuron to keep just two. Notice that the neural network is now incapable of finding a good solution - why that is?
Set the number of neurons to eight, and train the network several times. Has the training time (time to convergence) improved? Why that is?
Select the spiral dataset (the bottom-right dataset under “DATA”), and change the network architecture to have four hidden layers with eight neurons each. Notice that training takes much longer and often gets stuck on plateaus for long periods of time. Also notice that the neurons in the highest layers (on the right) tend to evolve faster than the neurons in the lowest layers (on the left). Can you explain how this may be related to gradient flow through the network?
Problem Set 2 (20 points)
(5 points) Submit your notebook URL that allows this notebook to be executed.
(15 points) Start reducing the number of cats in the dataset and plot the accuracy of the predicting the cat class as the population of cats becomes 90%, 70%, 50%, 30%, 10% of the original. For each population size present the hyperparameter optimized result using AutoKeras. Explain your findings.
Problem Set 3 (25 points)
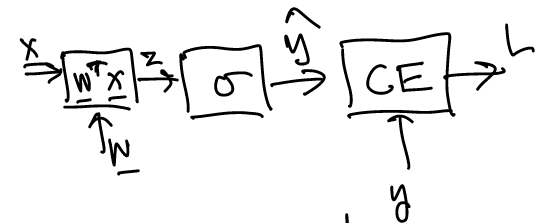
Assuming that \(x \in R^n\), backpropagate the following network to find
\[\frac{\partial L}{\partial \mathbf w}\]