Logistic Regression with SGD on GMM Data: When PCA Helps (Two Regimes)

This notebook creates two synthetic binary datasets from a Gaussian Mixture Model (GMM):

1. Low-noise regime (few noisy dims, strong class separation, ample data) — PCA has little effect.
2. High-noise regime (many noisy dims, weaker separation, fewer samples) — PCA clearly improves performance.

For each regime we: - Generate data (informative 2D subspace + noisy dimensions). - Train logistic regression with SGD on raw features and on PCA-reduced features. - Report Accuracy and AUC on the test set. - Plot ROC curves and decision surface in 2D PC space. - Show the PCA explained variance.

Setup

import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import TensorDataset, DataLoader
import matplotlib.pyplot as plt

torch.manual_seed(11)
np.random.seed(11)


def train_test_split(X, y, test_size=0.3, shuffle=True, seed=0):
    n = X.shape[0]
    idx = np.arange(n)
    if shuffle:
        rng = np.random.default_rng(seed)
        rng.shuffle(idx)
    n_test = int(round(test_size * n))
    test_idx = idx[:n_test]
    train_idx = idx[n_test:]
    return X[train_idx], X[test_idx], y[train_idx], y[test_idx]


def standardize_fit(X):
    mu = X.mean(axis=0, keepdims=True)
    std = X.std(axis=0, keepdims=True) + 1e-8
    return mu, std


def standardize_transform(X, mu, std):
    return (X - mu) / std


def auc_roc(scores, labels):
    scores = np.asarray(scores).ravel()
    labels = np.asarray(labels).astype(int).ravel()
    order = np.argsort(-scores, kind="mergesort")
    y = labels[order]
    P = y.sum()
    N = len(y) - P
    if P == 0 or N == 0:
        return float("nan")
    tps = np.cumsum(y)
    fps = np.cumsum(1 - y)
    tpr = tps / P
    fpr = fps / N
    return float(np.trapz(tpr, fpr))


def roc_curve(scores, labels):
    scores = np.asarray(scores).ravel()
    labels = np.asarray(labels).astype(int).ravel()
    order = np.argsort(-scores, kind="mergesort")
    y = labels[order]
    P = y.sum()
    N = len(y) - P
    tps = np.cumsum(y)
    fps = np.cumsum(1 - y)
    tpr = tps / (P + 1e-12)
    fpr = fps / (N + 1e-12)
    return fpr, tpr

GMM data generator

def make_gmm_binary(
    n_per_class=1000, d_total=20, d_informative=2, class_sep=2.5, noise_std=1.0, seed=0, random_rotate=True
):
    rng = np.random.default_rng(seed)

    sep = class_sep
    mus0 = np.array([[-sep, 0.0], [0.0, -sep]])
    mus1 = np.array([[sep, 0.0], [0.0, sep]])
    cov_inf = np.array([[1.0, 0.3], [0.3, 1.0]])

    def sample_class(mus, n):
        z = rng.integers(0, len(mus), size=n)
        X2 = np.stack([rng.multivariate_normal(mus[k], cov_inf) for k in z], axis=0)
        return X2

    X0_inf = sample_class(mus0, n_per_class)
    X1_inf = sample_class(mus1, n_per_class)

    d_noise = max(0, d_total - d_informative)
    if d_noise > 0:
        X0_noise = rng.normal(0.0, noise_std, size=(n_per_class, d_noise))
        X1_noise = rng.normal(0.0, noise_std, size=(n_per_class, d_noise))
        X0 = np.concatenate([X0_inf, X0_noise], axis=1)
        X1 = np.concatenate([X1_inf, X1_noise], axis=1)
    else:
        X0 = X0_inf
        X1 = X1_inf

    X = np.vstack([X0, X1]).astype(np.float32)
    y = np.concatenate([np.zeros(n_per_class), np.ones(n_per_class)]).astype(np.int64)

    if random_rotate:
        Q, _ = np.linalg.qr(rng.normal(size=(d_total, d_total)))
        X = (X @ Q).astype(np.float32)

    return X, y

PCA (Torch SVD)

def pca_fit_torch(X_np):
    Xc = X_np - X_np.mean(axis=0, keepdims=True)
    Xc_t = torch.from_numpy(Xc)
    U, S, Vh = torch.linalg.svd(Xc_t, full_matrices=False)
    n = X_np.shape[0]
    ev = (S**2) / (n - 1)
    evr = ev / ev.sum()
    components = Vh.numpy()
    mean_vec = X_np.mean(axis=0, keepdims=True)
    return components, evr.numpy(), mean_vec


def pca_transform(X_np, components, k, mean_vec):
    Xc = X_np - mean_vec
    W = components[:k].T
    return (Xc @ W).astype(np.float32)

Logistic regression (SGD)

class LogisticReg(nn.Module):
    def __init__(self, in_dim):
        super().__init__()
        self.lin = nn.Linear(in_dim, 1)

    def forward(self, x):
        return self.lin(x).squeeze(-1)


def train_logreg_sgd(Xtr_np, ytr_np, Xte_np, yte_np, lr=5e-3, epochs=300, batch_size=256, l2=2e-4):
    Xtr_t = torch.from_numpy(Xtr_np.astype(np.float32))
    ytr_t = torch.from_numpy(ytr_np.astype(np.float32))
    Xte_t = torch.from_numpy(Xte_np.astype(np.float32))
    yte_t = torch.from_numpy(yte_np.astype(np.float32))

    model = LogisticReg(in_dim=Xtr_t.shape[1])
    opt = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=l2)
    loss_fn = nn.BCEWithLogitsLoss()

    ds = TensorDataset(Xtr_t, ytr_t)
    dl = DataLoader(ds, batch_size=batch_size, shuffle=True)

    model.train()
    for ep in range(1, epochs + 1):
        running = 0.0
        for xb, yb in dl:
            logits = model(xb)
            loss = loss_fn(logits, yb)
            opt.zero_grad()
            loss.backward()
            opt.step()
            running += loss.item() * xb.size(0)
        if ep % 60 == 0:
            print(f"epoch {ep:4d} | loss: {running / len(ds):.4f}")

    model.eval()
    with torch.no_grad():
        logits_te = model(Xte_t).numpy()
    prob_te = 1.0 / (1.0 + np.exp(-logits_te))
    pred_te = (prob_te >= 0.5).astype(int)
    acc_te = (pred_te == yte_np).mean()
    auc_te = auc_roc(prob_te, yte_np)
    return model, acc_te, auc_te, prob_te

Regime A — Low-noise (PCA expected little effect)

params_A = dict(n_per_class=120000, d_total=100, d_informative=2, class_sep=2.5, noise_std=0.5, seed=1)
XA, yA = make_gmm_binary(**params_A)

XA_tr, XA_te, yA_tr, yA_te = train_test_split(XA, yA, test_size=0.3, shuffle=True, seed=123)
muA, stdA = standardize_fit(XA_tr)
XA_trs = standardize_transform(XA_tr, muA, stdA)
XA_tes = standardize_transform(XA_te, muA, stdA)

model_A_raw, acc_A_raw, auc_A_raw, prob_A_raw = train_logreg_sgd(XA_trs, yA_tr, XA_tes, yA_te)
print(f"[Regime A] Raw: acc={acc_A_raw:.3f}, AUC={auc_A_raw:.3f}")

components_A, evr_A, mean_A = pca_fit_torch(XA_trs.copy())
k95_A = int(np.searchsorted(np.cumsum(evr_A), 0.95) + 1)
XA_tr_pca = pca_transform(XA_trs, components_A, k95_A, mean_A)
XA_te_pca = pca_transform(XA_tes, components_A, k95_A, mean_A)

model_A_pca, acc_A_pca, auc_A_pca, prob_A_pca = train_logreg_sgd(XA_tr_pca, yA_tr, XA_te_pca, yA_te)
print(f"[Regime A] PCA@95% (k={k95_A}): acc={acc_A_pca:.3f}, AUC={auc_A_pca:.3f}")

epoch   60 | loss: 0.1522
epoch  120 | loss: 0.1522
epoch  180 | loss: 0.1522
epoch  240 | loss: 0.1522
epoch  300 | loss: 0.1522
[Regime A] Raw: acc=0.939, AUC=0.985
epoch   60 | loss: 0.1530
epoch  120 | loss: 0.1530
epoch  180 | loss: 0.1530
epoch  240 | loss: 0.1530
epoch  300 | loss: 0.1530
[Regime A] PCA@95% (k=91): acc=0.938, AUC=0.985

Regime A — PCA cumulative explained variance

plt.figure(figsize=(6, 4))
plt.plot(np.arange(1, len(evr_A) + 1), np.cumsum(evr_A), marker="o")
plt.xlabel("number of PCs")
plt.ylabel("cumulative explained variance")
plt.title("Regime A: PCA cumulative explained variance (train)")
plt.show()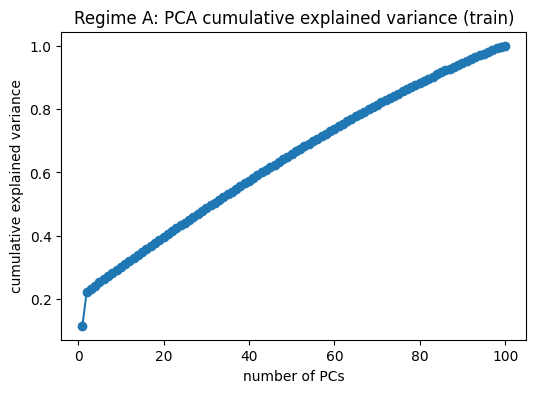

Regime A — ROC (raw vs PCA)

fpr_A_raw, tpr_A_raw = roc_curve(prob_A_raw, yA_te)
fpr_A_pca, tpr_A_pca = roc_curve(prob_A_pca, yA_te)

plt.figure(figsize=(6, 5))
plt.plot(fpr_A_raw, tpr_A_raw, label=f"Raw (AUC={auc_A_raw:.3f})")
plt.plot(fpr_A_pca, tpr_A_pca, label=f"PCA@95% (AUC={auc_A_pca:.3f})")
plt.plot([0, 1], [0, 1], linestyle="--")
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.title("Regime A: ROC")
plt.legend()
plt.show()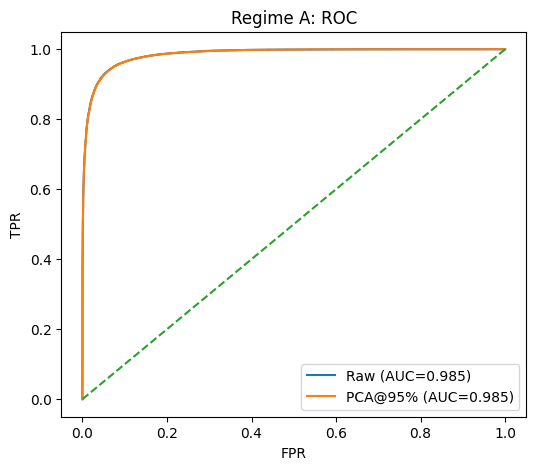

Regime B — High-noise (PCA expected to help)

params_B = dict(n_per_class=120000, d_total=200, d_informative=2, class_sep=2.5, noise_std=0.5, seed=2)
XB, yB = make_gmm_binary(**params_B)

XB_tr, XB_te, yB_tr, yB_te = train_test_split(XB, yB, test_size=0.3, shuffle=True, seed=123)
muB, stdB = standardize_fit(XB_tr)
XB_trs = standardize_transform(XB_tr, muB, stdB)
XB_tes = standardize_transform(XB_te, muB, stdB)

model_B_raw, acc_B_raw, auc_B_raw, prob_B_raw = train_logreg_sgd(XB_trs, yB_tr, XB_tes, yB_te)
print(f"[Regime B] Raw: acc={acc_B_raw:.3f}, AUC={auc_B_raw:.3f}")

components_B, evr_B, mean_B = pca_fit_torch(XB_trs.copy())
k95_B = int(np.searchsorted(np.cumsum(evr_B), 0.95) + 1)
XB_tr_pca = pca_transform(XB_trs, components_B, k95_B, mean_B)
XB_te_pca = pca_transform(XB_tes, components_B, k95_B, mean_B)

model_B_pca, acc_B_pca, auc_B_pca, prob_B_pca = train_logreg_sgd(XB_tr_pca, yB_tr, XB_te_pca, yB_te)
print(f"[Regime B] PCA@95% (k={k95_B}): acc={acc_B_pca:.3f}, AUC={auc_B_pca:.3f}")

epoch   60 | loss: 0.1532
epoch  120 | loss: 0.1532
epoch  180 | loss: 0.1532
epoch  240 | loss: 0.1532
epoch  300 | loss: 0.1532
[Regime B] Raw: acc=0.939, AUC=0.986
epoch   60 | loss: 0.1536
epoch  120 | loss: 0.1536
epoch  180 | loss: 0.1536
epoch  240 | loss: 0.1536
epoch  300 | loss: 0.1536
[Regime B] PCA@95% (k=185): acc=0.939, AUC=0.985

Regime B — PCA cumulative explained variance

plt.figure(figsize=(6, 4))
plt.plot(np.arange(1, len(evr_B) + 1), np.cumsum(evr_B), marker="o")
plt.xlabel("number of PCs")
plt.ylabel("cumulative explained variance")
plt.title("Regime B: PCA cumulative explained variance (train)")
plt.show()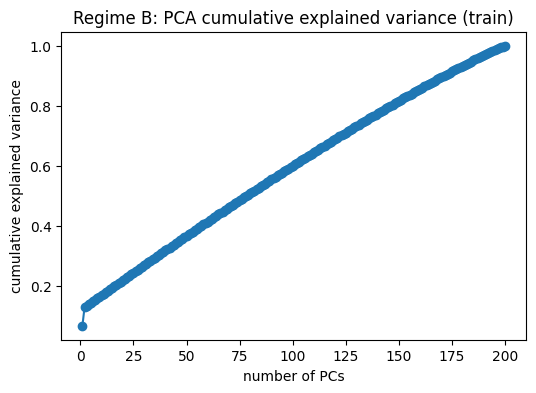

Regime B — ROC (raw vs PCA)

fpr_B_raw, tpr_B_raw = roc_curve(prob_B_raw, yB_te)
fpr_B_pca, tpr_B_pca = roc_curve(prob_B_pca, yB_te)

plt.figure(figsize=(6, 5))
plt.plot(fpr_B_raw, tpr_B_raw, label=f"Raw (AUC={auc_B_raw:.3f})")
plt.plot(fpr_B_pca, tpr_B_pca, label=f"PCA@95% (AUC={auc_B_pca:.3f})")
plt.plot([0, 1], [0, 1], linestyle="--")
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.title("Regime B: ROC")
plt.legend()
plt.show()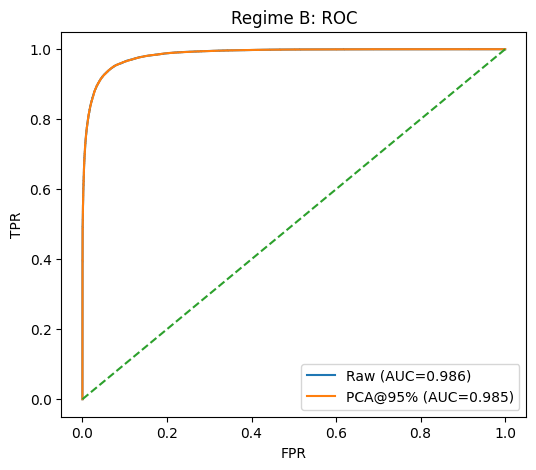

Regime B — Decision surface on top-2 PCs

def train_logreg_return_model(Xtr_np, ytr_np, lr=5e-3, epochs=200, batch_size=256, l2=2e-4):
    Xtr_t = torch.from_numpy(Xtr_np.astype(np.float32))
    ytr_t = torch.from_numpy(ytr_np.astype(np.float32))
    model = LogisticReg(in_dim=Xtr_t.shape[1])
    opt = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=l2)
    loss_fn = nn.BCEWithLogitsLoss()
    ds = TensorDataset(Xtr_t, ytr_t)
    dl = DataLoader(ds, batch_size=batch_size, shuffle=True)
    model.train()
    for ep in range(epochs):
        for xb, yb in dl:
            logits = model(xb)
            loss = loss_fn(logits, yb)
            opt.zero_grad()
            loss.backward()
            opt.step()
    return model


XB_tr_pca2 = pca_transform(XB_trs, components_B, 2, mean_B)
model_B_pca2_viz = train_logreg_return_model(XB_tr_pca2, yB_tr, epochs=200)

xx, yy = np.meshgrid(
    np.linspace(XB_tr_pca2[:, 0].min() - 1.0, XB_tr_pca2[:, 0].max() + 1.0, 200),
    np.linspace(XB_tr_pca2[:, 1].min() - 1.0, XB_tr_pca2[:, 1].max() + 1.0, 200),
)
grid = np.stack([xx.ravel(), yy.ravel()], axis=1).astype(np.float32)
with torch.no_grad():
    logits_grid = model_B_pca2_viz.lin(torch.from_numpy(grid)).numpy().reshape(xx.shape)
    probs_grid = 1.0 / (1.0 + np.exp(-logits_grid))

plt.figure(figsize=(6, 5))
plt.contourf(xx, yy, probs_grid, levels=20, alpha=0.3)
plt.scatter(XB_tr_pca2[:, 0], XB_tr_pca2[:, 1], s=10, c=yB_tr, alpha=0.6)
plt.title("Regime B: Decision surface (logistic on top-2 PCs)")
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()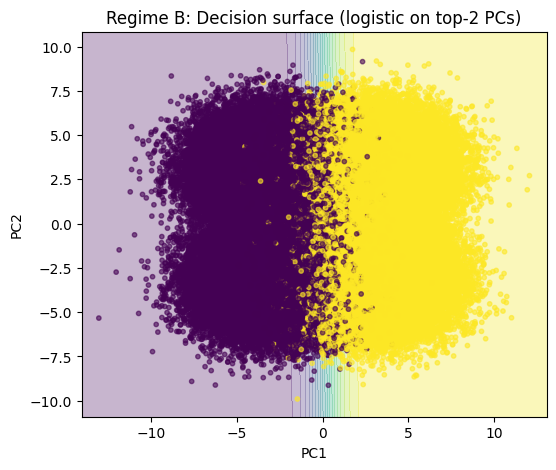

Summary

• Regime A (low noise): Logistic regression on raw features already performs near-optimally; PCA changes little.
• Regime B (high noise): Raw high-dimensional noise degrades logistic regression; PCA denoises and reduces dimension, yielding higher accuracy/AUC.
• This illustrates that PCA is not a magic bullet, but it helps when signal lies in a low-dimensional subspace and noise dominates elsewhere.