Camera Model
Homogeneous coordinates

All of us are familiar with heterogenous coordinates that describe points in the Cartesian space as a tuple of three numbers\((x,y,z)\). In computer vision and in computer graphics, we need to work in another space called the projective space where the coordinates of a 3D point is four dimensional and where the additional dimension\(w\)is called the scale.
The four coordinates in this space are called homogeneous coordinates.
In 2D space, a point\((x, y)\)can be represented in homogeneous coordinates as\((x, y, 1)\). This extra coordinate allows for more flexible transformations, such as translation, which are not easily represented in Cartesian coordinates.
For example, the point\((2, 3)\)in Cartesian coordinates can be represented as\((2, 3, 1)\)in homogeneous coordinates. If we want to translate this point by\((dx, dy) = (1, 2)\), we can use the following transformation matrix:
\[ \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} \]
Applying this matrix to the point\((2, 3, 1)\):
\[ \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 + 1 \\ 3 + 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \\ 1 \end{bmatrix} \]
So, the translated point is\((3, 5)\)in Cartesian coordinates.
Lenses
The effect of refraction
Camera Calibration and 3D Reconstruction
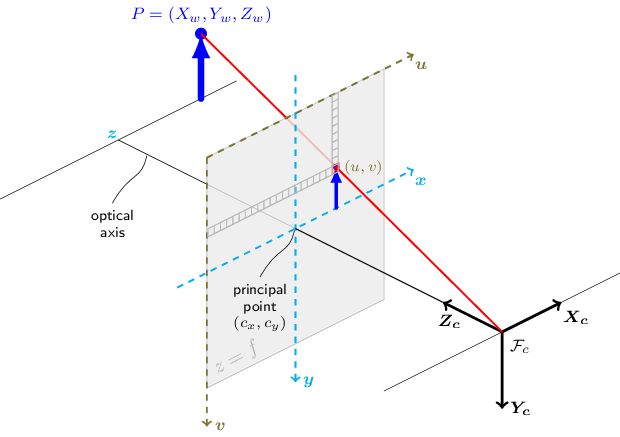
The functions in this section use a pinhole camera model. The view of a scene is obtained by projecting a 3D point\(P_w\)into the image plane using a perspective transformation, forming the corresponding pixel\(p\). Both\(P_w\)and\(p\)are represented in homogeneous coordinates.
For succinct notation, we often refer to vectors instead of homogeneous vectors. Below is the distortion-free projective transformation of the pinhole camera model:
\[s \; p = A \begin{bmatrix} R|t \end{bmatrix} P_w,\]
where: -\(P_w\): 3D point in the world coordinate system. -\(p\): 2D pixel in the image plane. -\(A\): Camera intrinsic matrix. -\(R\),\(t\): Rotation and translation matrices for the world-to-camera coordinate transformation. -\(s\): Arbitrary scaling factor.
Camera Intrinsic Matrix
The intrinsic matrix\(A\), also referred to as\(K\), projects 3D points in the camera coordinate system to 2D pixel coordinates:
\[p = A P_c,\]
where:
\[A = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix},\]
and\(f_x\),\(f_y\)are focal lengths in pixel units, and\((c_x, c_y)\)is the principal point (usually near the image center).
Extrinsic Parameters
The rotation-translation matrix\([R|t]\)transforms world coordinates to camera coordinates:
\[P_c = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} P_w.\]
Combining intrinsic and extrinsic parameters gives:
\[s \; p = A \begin{bmatrix} R|t \end{bmatrix} P_w.\]
Real-World Lenses
Real lenses introduce distortions (radial and tangential). The model extends as:
\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x x'' + c_x \\ f_y y'' + c_y \end{bmatrix},\]
where:
\[\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} x' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2 p_1 x' y' + p_2 (r^2 + 2 x'^2) \\ y' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' \end{bmatrix},\]
with\(r^2 = x'^2 + y'^2\).
Homogeneous Coordinates
Homogeneous coordinates represent points at infinity with finite coordinates and simplify transformations:
- Cartesian to homogeneous:
\[ \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \rightarrow \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}. \] - Homogeneous to Cartesian:
\[ \begin{bmatrix} X \\ Y \\ W \end{bmatrix} \rightarrow \begin{bmatrix} X / W \\ Y / W \end{bmatrix}, \quad \text{if } W \ne 0. \]
Applications
The functions support: - Projecting 3D points onto the image plane. - Estimating extrinsic parameters. - Camera calibration from known patterns. - Stereo calibration and rectification.
Fisheye Camera Model
The fisheye model accounts for radial distortions using:
\[\theta_d = \theta (1 + k_1 \theta^2 + k_2 \theta^4 + k_3 \theta^6 + k_4 \theta^8).\]
The final pixel coordinates are given by:
\[\begin{aligned} u &= f_x (x' + \alpha y') + c_x, \\ v &= f_y y' + c_y. \end{aligned}\]
Notes
- Intrinsic parameters remain valid across resolutions if scaled appropriately.
- Example calibration codes can be found in OpenCV source (e.g.,
3calibration.cpp,stereo_calib.cpp).

