Introduction to Transfer Learning#
Transfer Learning is a foundational approach to learning.
In this section we borrow heavily from this article and connect the transfer learng to multitask learning and to continual learning. We will use the binary classification as the main task of interest.
Transfer learning involves the concepts of a domain and a task. A domain \(\mathcal D\) consists of a feature space \(\mathcal X\) and a marginal probability distribution \(p(\mathbf x)\) where
Given a domain, \(\mathcal D = \{\mathcal X, p(\mathbf x) \}\) and task \(\mathcal T\) consists of a label space \(\mathcal Y\) and a conditional probability distribution \(p(\mathbf y| \mathbf x)\) that is typically learned from the training data \((\mathbf x_i, \mathbf y_i)\).
Given a source domain \(\mathcal D_S = \{\mathcal X_S, p(\mathbf x_S) \}\), a corresponding source task \(\mathcal T_S\) and a target domain \(\mathcal D_T = \{\mathcal X_T, p(\mathbf x_T) \}\) with a corresponding target task \(\mathcal T_T\), the objective of transfer learning is to learn the target conditional probability distribution \(p(\mathbf y_T| \mathbf x_T)\) from the information gained from \(\mathcal D_S\) and \(\mathcal T_S\).
We assume that a far smaller number of labeled examples of the target domain exist as compared to the labelled examples of the source domain.
There are three main possibilities in our binary classification problem.
\(\mathcal X_S \neq \mathcal X_T\). For example the domain of images of nature and the domain of images of houses. The domain of documents in English and in French. The domain of numbers in Arabic and the domain of numbers in Latin.
\(p(\mathbf x_S) \neq p(\mathbf x_T)\). Both distributions are generated by the same domain but the marginals are different and therefore this case is known as domain adaptation. For example the domain of English documents with marginals obtained from documents of different topics. Another example is shown here where the marginals are different because different people have different physiologies in their hands and EMG signals are sensed for a person sometimes quite differently than others. Finally the classic domain adaptation example: spoken English with the marginals referring to different accents.
\(p(\mathbf y_S| \mathbf x_S) \neq p(\mathbf y_T| \mathbf x_T)\) This is the most common scenario where we use the task we learned in the source domain to improve our learning of the target domain.
Take for example the case of a pretrained network on MS COCO dataset that includes cars amongst 79 other classes. We now want to train a network to classify sports-cars. These tasks are very similar, even partly overlapping, so you should try to reuse parts of the first network.
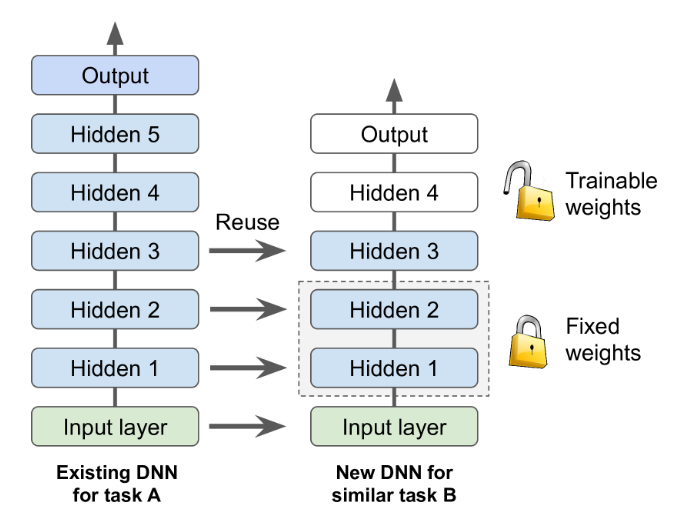
More generally, transfer learning will work best when the inputs have similar low-level features.
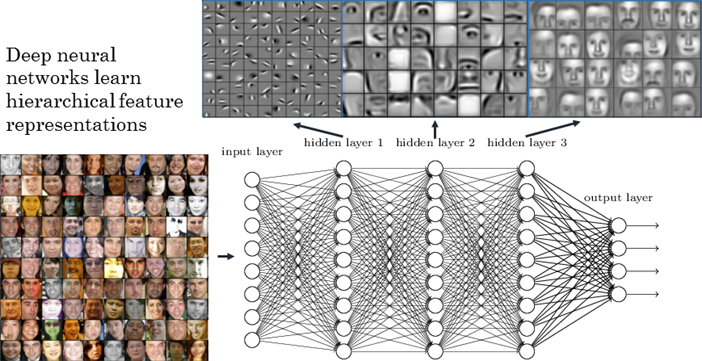
Note
Please note that the diagram above is used for illustration purposes only. DNNs as shown above do not work very well with transfer learning. In your mind replace the DNN with CNN.
Because these low-level features are captured in the lower layers of the network as shown below, we reuse the base of the network. Similarly, the upper hidden layers of the original model are less likely to be as useful as the lower layers, since the high-level features that are most useful for the new task may differ significantly from the ones that were most useful for the original task. You want to find the right number of layers to reuse.
The output layer of the original model should usually be replaced because it is most likely not useful at all for the new task, and it generally does not even have the right number of outputs.
Fine Tuning#
A complementary approach is fine-tuning where we allow a upper subset of the base network to train while continue to keep frozen the weights of the bottom of the base. See this for an example for a fine-tuning approach for the problem of instance segmentation.
Workshop#
The application of transfer learning in Keras is demonstrated here.
